COMMunication
RESearch.NET

User Tools

Site Tools

You are here: index » c » ms » 2024 » schedule
Trace: • twoway_anova • schedule • schedule • 2023 • 2021 • schedule • 2016 • group_02 • schedule • schedule
c:ms:2024:schedule

This is an old revision of the document!

Table of Contents

통계에 대한 기초적인 이해
가설과 가설검증

  • 가설의 종류와 그 종류에 따른 통계분석법
    • z-test
    • t-test
    • ANOVA
    • Factorial ANOVA
    • correlation
    • regression
    • multiple regression
    • factor analysis
    • . . .
  • 위를 위해서 꼭 이해해야 할 것들
    • Variance
    • Standard Deviation
    • Standard Error (Standard Deviation of Sample Means)
    • Hypothesis Testing

R Cookbook
Chapter 1 Getting Started and Getting Help
Chapter 2 Some Basics
Chapter 3 Navigating the Software
Chapter 4 Input and Output
Chapter 5 Data Structures
Chapter 6 Data Transformations
Chapter 7 Strings and Dates
Chapter 8 Probability
Chapter 9 General Statistics
Chapter 10 Graphics
Chapter 11 Linear Regression and ANOVA
Chapter 12 Useful Tricks
Chapter 13 Beyond Basic Numerics and Statistics
Chapter 14 Time Series Analysis

이전 페이지

  • Week 01: March 4, 6
  • Week 02: March 11, 13
  • Week 03: March 18, 20
  • Week 04: March 25, 27
  • Week 05: April 1, April 3
  • Week 06: April 8, 10
  • Week 07: April 15, 15
  • Week 08: April 22, 24
  • Week 09: April 29, May 1
  • Week 10: May 6, 8
  • Week 11: May 13, 15
  • Week 12: May 20, 22
  • Week 13: May 27, 28
  • Week 14: June 3, June 5
  • Week 15: June 10, 12
  • Week 16: June 17, 19

Week01

Course Introduction –> syllabus

ideas and concepts

동영상 (R 관련)

Introduction to R and others

  1. Downloading and Installing R
    1. the_r_project_for_statistical_computing
    2. r, getting started
  2. Starting R
  3. Entering Commands
  4. Exiting from R
  5. Interrupting R
  6. Viewing the Supplied Documentation
  7. Getting Help on a Function
  8. Searching the Supplied Documentation
  9. Getting Help on a Package
  10. Searching the Web for Help
  11. Finding Relevant Functions and Packages
  12. Searching the Mailing Lists
  13. Submitting Questions to the Mailing Lists

동영상 (통계관련 샘플링에 대한 설명)

기본용어
기술통계 (descriptive statistics)
추론통계 (inferential statistics)
아래의 개념은 샘플링 문서를 먼저 볼것

  • sampling methods
    • probability
    • non-probability

가설 (hypothesis)

  • 차이와 연관 (difference and association)

변인 (variables)

Assignment

etc

What's normal distribution? 

?rnorm
?pnorm
?qnorm
. . . .
rnorm(40,100,10) 
rnorm(20,0,1)
rnorm(20) 
rnorm2 <- function(n,mean,sd) { mean+sd*scale(rnorm(n)) }

set.seed(101)
a <- rnorm(1000,100,10)
mean(a)
sd(a)

b <- rnorm2(1000,100,10)
mean(b)
sd(b)

Week02

Concepts and ideas

Sampling
가설
지난 동영상 리캡 및 가설에 대한 소개
가설에 대한 소개 및 설명
가설이 만들어지는 이유
가설의 예
변인의 종류와 변인측정의수준

Some basics

  1. Introduction
  2. Printing Something
  3. Setting Variables
  4. Listing Variables
  5. Deleting Variables
  6. Creating a Vector
  7. Computing Basic Statistics
  8. Creating Sequences
  9. Comparing Vectors
  10. Selecting Vector Elements
  11. Performing Vector Arithmetic
  12. Getting Operator Precedence Right
  13. Defining a Function
  14. Typing Less and Accomplishing More
  15. Avoiding Some Common Mistakes

from the previous lecture (research question and hypothesis)

Qs

normal_distribution 

# normal distribution 
# see the above [[:normal_distribution]] doc 
# dnorm = density of normal distribution 
# pnorm = percentile of normal distribution
# qnorm = quantile of normal distribution
# rnorm = random sampling of normal distribution
dnorm(0,0,1)
x <- seq(-5, 5, length=11)
span <- c(x)
span 
dnorm(span, 0,1)
plot(dnorm(span,0,1))

pnorm(0,0,1)
pnorm(1,0,1)
pnorm(2)
pnorm(3)

# volume of the intersection 
pnorm(1)-pnorm(-1)
pnorm(2)-pnorm(-2)
pnorm(3)-pnorm(-3)

# qnorm
qnorm(0.84134478,0,1)
qnorm(0.97724988888)
qnorm(0.9986501)
> dnorm(0,0,1)
[1] 0.3989423
> x <- seq(-5, 5, length=11)
> span <- c(x)
> span 
 [1] -5 -4 -3 -2 -1  0  1  2  3  4  5
> dnorm(span, 0,1)
 [1] 1.486720e-06 1.338302e-04 4.431848e-03 5.399097e-02 2.419707e-01 3.989423e-01 2.419707e-01
 [8] 5.399097e-02 4.431848e-03 1.338302e-04 1.486720e-06
> plot(dnorm(span,0,1))
> 
> pnorm(0,0,1)
[1] 0.5
> pnorm(1,0,1)
[1] 0.8413447
> pnorm(2)
[1] 0.9772499
> pnorm(3)
[1] 0.9986501
> 
> # volume of the intersection 
> pnorm(1)-pnorm(-1)
[1] 0.6826895
> pnorm(2)-pnorm(-2)
[1] 0.9544997
> pnorm(3)-pnorm(-3)
[1] 0.9973002
> 
> # qnorm
> qnorm(0.84134478,0,1)
[1] 1
> qnorm(0.97724988888)
[1] 2
> qnorm(0.9986501)
[1] 3
> 
> 0.05/2
[1] 0.025
> qnorm(1-0.025)
[1] 1.959964
> qnorm(0.025)
[1] -1.959964

> 0.01/2
[1] 0.005
> 1-(0.01/2)
[1] 0.995
> qnorm(1-0.005)
[1] 2.575829
> qnorm(0.005)
[1] -2.575829

> 0.32/2
[1] 0.16
> qnorm(1-0.16) # = 0.84
[1] 0.9944579
> qnorm(0.16)
[1] -0.9944579
>

Assignment

Week03

3주차 온라인 강의 동영상은 4주에 걸쳐서 보시기 바랍니다. 즉, 4주 중에 따로 동영상 올리지 않습니다.

—–

—–
Howell, Ch. 4 내용 중 Variance와 (분산) Standard deviation은 (표준편차는) 이후 통계 검증방법을 이해하는데 기초가 되는 중요한 내용이니 꼭 숙지하시기 바랍니다.

Concepts and ideas

Navigating software

  1. Introduction
  2. Getting and Setting the Working Directory
  3. Saving Your Workspace
  4. Viewing Your Command History
  5. Saving the Result of the Previous Command
  6. Displaying the Search Path
  7. Accessing the Functions in a Package
  8. Accessing Built-in Datasets
  9. Viewing the List of Installed Packages
  10. Installing Packages from CRAN
  11. Setting a Default CRAN Mirror
  12. Suppressing the Startup Message
  13. Running a Script
  14. Running a Batch Script
  15. Getting and Setting Environment Variables
  16. Locating the R Home Directory
  17. Customizing R

Mean
Mode
Median
Variance
Standard Deviation

+-1 sd = 68% = +-1 sd
+-2 sd = 95% = +-1.96 sd
+-3 sd = 99% (99.7%) = +-3 sd

표준점수 (unit with a standard deviation) = z score

Sampling distribution via random sampling

Central Limit Theorem 

# +-1SD = 68% 
# +-2SD = 95% 
# +-3SD = 99% 라고 했지만 
# pnorm(2) = ? 
pnorm(2)
pnorm(2) - pnorm(-2)
pnorm(90,70,10)
pnorm(90,70,10) - pnorm(50,70,10)
pnorm(3) - pnorm(-3)

# 95%를 마춰서 생각하려면 
qnorm(0.975) # .05의 (1-0.95) 오른쪽 반 
qnorm(0.025) # 왼쪽 반
s2.h <- qnorm(.975) # environment panel (r) 체크할 것 
s2.l <- qnorm(.025)
pnorm(s2.h) - pnorm(s2.l) # 정확히 95%

# 1%의 반반씩 생각해보기
s3.h <- qnorm(0.995)
s3.l <- qnorm(0.005)
pnorm(s3.h) - pnorm(s3.l)

# for variance of sample means
# see the [[:sampling distribution in r]]

see the sampling distribution in r

Assignment

Week04

동영상 시청

Class Activity

Lecture materials for this week

Concepts and ideas

Input and output

  1. Introduction
  2. Entering Data from the Keyboard
  3. Printing Fewer Digits (or More Digits)
  4. Redirecting Output to a File
  5. Listing Files
  6. Dealing with “Cannot Open File” in Windows
  7. Reading Fixed-Width Records
  8. Reading Tabular Data Files
  9. Reading from CSV Files
  10. Writing to CSV Files
  11. Reading Tabular or CSV Data from the Web
  12. Reading Data from HTML Tables
  13. Reading Files with a Complex Structure
  14. Reading from MySQL Databases
  15. Saving and Transporting Objects

20230329-102748.jpeg
아래 두번째 그림은 population의 평균이 102 일 때
400명을 (1600명이 아니라) 샘플로 취했을 때의
샘플평균들의 집합을 그린것입니다.
20230329-102811.jpeg

Assignment

Announcement Quiz 01

다음 주 수요일 (5주차 두번째시간) 퀴즈 있습니다.
퀴즈 범위는

  • 5주차까지 언급된 모든 동영상
  • R 과 관련해서는 동영상 내용만 포함합니다.

문서

  • 시험문제는 4지선다 혹은 단답식 답입니다.
  • 문제는 모두 50문제 정도입니다.

Week05

Concepts and ideas

Data Structures

  1. Introduction
  2. Appending Data to a Vector
  3. Inserting Data into a Vector
  4. Understanding the Recycling Rule
  5. Creating a Factor (Categorical Variable)
  6. Combining Multiple Vectors into One Vector and a Factor
  7. Creating a List
  8. Selecting List Elements by Position
  9. Selecting List Elements by Name
  10. Building a Name/Value Association List
  11. Removing an Element from a List
  12. Flatten a List into a Vector
  13. Removing NULL Elements from a List
  14. Removing List Elements Using a Condition
  15. Initializing a Matrix
  16. Performing Matrix Operations
  17. Giving Descriptive Names to the Rows and Columns of a Matrix
  18. Selecting One Row or Column from a Matrix
  19. Initializing a Data Frame from Column Data
  20. Initializing a Data Frame from Row Data
  21. Appending Rows to a Data Frame
  22. Preallocating a Data Frame
  23. Selecting Data Frame Columns by Position
  24. Selecting Data Frame Columns by Name
  25. Selecting Rows and Columns More Easily
  26. Changing the Names of Data Frame Columns
  27. Editing a Data Frame
  28. Removing NAs from a Data Frame
  29. Excluding Columns by Name
  30. Combining Two Data Frames
  31. Merging Data Frames by Common Column
  32. Accessing Data Frame Contents More Easily
  33. Converting One Atomic Value into Another
  34. Converting One Structured Data Type into Another

Assignment

#####
mu.pop <- 100
sd.pop <- 10

set.seed(101)
treated.group <- rnorm(16, 112, 10)
treated.group
m.tg <- mean(treated.group)
m.tg

# H1: m.tg =\ mu.pop (100) ?
# H0: if m.tg =\ mu.pop (100) 
# then
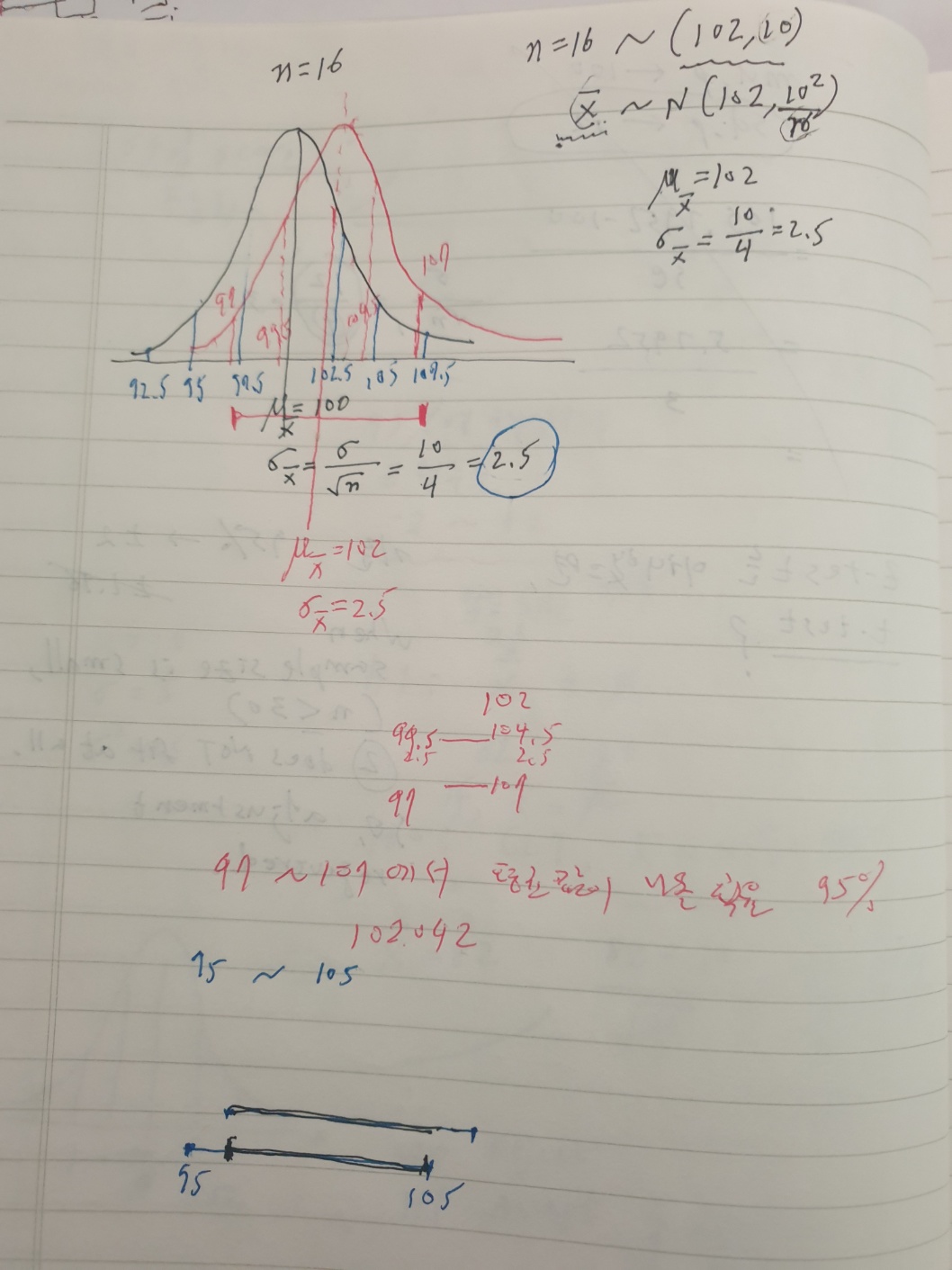
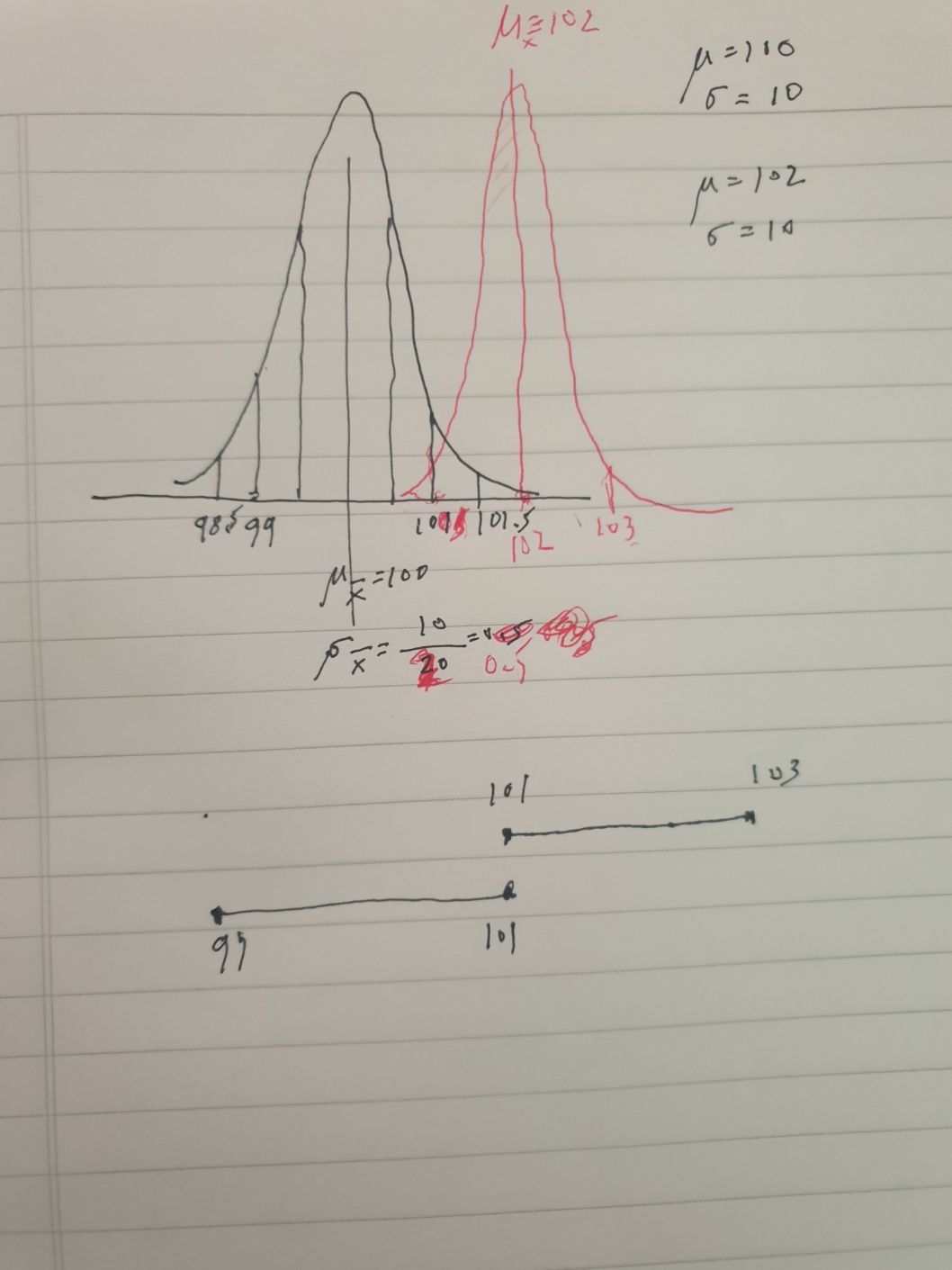
# n=16 Xbar ~ N(mu.pop, 25/4) 
# 즉 Xbar집합의 분산은 6.25 
# 표준편차는 (표준오차, se) 2.5
# 따라서 Xbar 집합의 평균을 중심으로한 
# 95% 범위는 pop.mu +- 2*(se)
# 즉, 100중 95는 95 ~ 105 사이에서 샘플의 평균이 나와야 함
# 즉, m.tg는 위의 범위에서 나와야 함. 그러나
# 나머지 5%는 95 밑이나 105 위에서 나올 수도 있음
# 그런데, m.tg = 113.0706
# 이를 근거로 영가설을 부정하고 
# 검증하고자 하는 연구가설을 채택함
# 즉, treated group 과 모집단의 평균은 다르다. 혹은 
# treated group은 모집단에서 추출될 수 있는 샘플이 아니라
# 다른 모집단에 속한 샘플이다 (95% 확신, 5% 에러마진)
se <- sqrt((sd.pop^2)/16)
qnorm(0.975,mean=100,sd=se)
# [1] 104.8999
qnorm(0.025,mean=100,sd=se)
# [1] 95.10009

# 그렇다면 mu.tg 값이 나올 확률은 몇일까?
pnorm(mu.tg, mean=100, sd=se)
# [1] 0.9999999
sscore <- (m.tg-mu.pop)/se
sscore
# [1] 5.22823 
1-pnorm(sscore,0,1)
# [1] 8.557037e-08
a <- 1-pnorm(sscore,0,1)
b <- pnorm(-sscore,0,1)
a
# [1] 8.557037e-08
b
# [1] 8.557037e-08
a+b
# [1] 1.711407e-07

# install.packages("BSDA")
# library(BSDA)
z.test(treated.group, mu=mu.pop, sigma.x=sd.pop) 

mu.pop <- 100
sd.pop <- 10

set.seed(100)
treated.group.2 <- rnorm(16, 102, 10)
treated.group.2
m.treated.group.2 <- mean(treated.group.2)
m.treated.group.2

# install.packages("BSDA")
# library(BSDA)
z.test(treated.group.2, mu=mu.pop, sigma.x=sd.pop) 

set.seed(100)
treated.group.2 <- rnorm(1600, 102, 10)
treated.group.2
m.treated.group.2 <- mean(treated.group.2)
m.treated.group.2

# install.packages("BSDA")
# library(BSDA)
z.test(treated.group.2, mu=mu.pop, sigma.x=sd.pop) 


> z.test(treated.group, mu=mu.pop, sigma.x=sd.pop) 

	One-sample z-Test

data:  treated.group
z = 5.2282, p-value = 1.711e-07
alternative hypothesis: true mean is not equal to 100
95 percent confidence interval:
 108.1707 117.9705
sample estimates:
mean of x 
 113.0706 

> 
# 위에서 . . . . z 값이 +_2 밖이면 영가설을 부정하고 
# 연구가설을 채택하게 된다
# 샘플 숫자가 작을 경우 위의 +-2 점수가 정확하지
# 않기 때문에 보정을 해주게 된다. 이 보정된 값은
# 샘플의 숫자에 따라서 (degrees of freedom) 달
# 라지게 된다

t-test
t distribution table
t-test in R

Week06

Concepts and ideas

이번 주 동영상

또한 R에서 데이터를 (테이블 혹은 어레이) 이용하여 function을 적용하는 것에 대해서 잘 익혀두시기 바랍니다. 이는 R cookbook의 아래 내용에 해당이 됩니다 (특히 sapply, tapply, by 등)

Data Transformations

  1. Introduction
  2. Splitting a Vector into Groups
  3. Applying a Function to Each List Element
  4. Applying a Function to Every Row
  5. Applying a Function to Every Column
  6. Applying a Function to Groups of Data
  7. Applying a Function to Groups of Rows
  8. Applying a Function to Parallel Vectors or Lists

Strings and Dates

week06 t-test and anova note 

# pnorm
# qnorm
# pt
# qt
percentage <- .975
df <- 99
t.critical <- qt(percentage, df) # sample size = df + 1 일 때, 95%에 해당하는 점수는?
t.critical

t.calculated <- 3.6
df <- 8
pt(t.calculated, df)

Announcement

Assignment

Week07

Concepts and ideas

Hypothesis testing
z-test

  • r 에서 qnorm(proportion) pnorm(z-score) function 이해 필요
  • z_score 참조

types of error

7주차 동영상

Probability calculation in R ← Probability in R cookbook (텍스트북)

Probability

  1. Introduction
  2. Counting the Number of Combinations
  3. Generating Combinations
  4. Generating Random Numbers
  5. Generating Reproducible Random Numbers
  6. Generating a Random Sample
  7. Generating Random Sequences
  8. Randomly Permuting a Vector
  9. Calculating Probabilities for Discrete Distributions
  10. Calculating Probabilities for Continuous Distributions
  11. Converting Probabilities to Quantiles
  12. Plotting a Density Function

w07 anova note

Assignment

8주차 퀴즈

8주차 정기시험기간 중에 2차 퀴즈

Week08

시험기간

Week09

Concepts and ideas

영상 ANOVA

위키페이지 참조

General Statistics

  1. Introduction
  2. Summarizing Your Data
  3. Calculating Relative Frequencies
  4. Tabulating Factors and Creating Contingency Tables
  5. Testing Categorical Variables for Independence
  6. Calculating Quantiles (and Quartiles) of a Dataset
  7. Inverting a Quantile
  8. Converting Data to Z-Scores
  9. Testing the Mean of a Sample (t Test)
  10. Forming a Confidence Interval for a Mean
  11. Forming a Confidence Interval for a Median
  12. Testing a Sample Proportion
  13. Forming a Confidence Interval for a Proportion
  14. Testing for Normality
  15. Testing for Runs
  16. Comparing the Means of Two Samples
  17. Comparing the Locations of Two Samples Nonparametrically
  18. Testing a Correlation for Significance
  19. Testing Groups for Equal Proportions
  20. Performing Pairwise Comparisons Between Group Means
  21. Testing Two Samples for the Same Distribution

vene . . . go or come

intervene

  • intervenient

convene

  • convention
  • convent
  • convenient

contravene
prevent
advent
circumvent

Assignment

Week10

Concepts and ideas

10주차 동영상입니다.

see w10.lecture.note

Assignment

Week11

Concepts and ideas

동영상 (총 5 개)

—-

w11.lecture.note

repeated measure ANOVA

correlation

regression
multiple regression
using dummy variables

getting started
basics
navigating in r
input output in r
data structures
data transformations

Graphics

  1. Introduction
  2. Creating a Scatter Plot
  3. Adding a Title and Labels
  4. Adding a Grid
  5. Creating a Scatter Plot of Multiple Groups
  6. Adding a Legend
  7. Plotting the Regression Line of a Scatter Plot
  8. Plotting All Variables Against All Other Variables
  9. Creating One Scatter Plot for Each Factor Level
  10. Creating a Bar Chart
  11. Adding Confidence Intervals to a Bar Chart
  12. Coloring a Bar Chart
  13. Plotting a Line from x and y Points
  14. Changing the Type, Width, or Color of a Line
  15. Plotting Multiple Datasets
  16. Adding Vertical or Horizontal Lines
  17. Creating a Box Plot
  18. Creating One Box Plot for Each Factor Level
  19. Creating a Histogram
  20. Adding a Density Estimate to a Histogram
  21. Creating a Discrete Histogram
  22. Creating a Normal Quantile-Quantile (Q-Q) Plot
  23. Creating Other Quantile-Quantile Plots
  24. Plotting a Variable in Multiple Colors
  25. Graphing a Function
  26. Pausing Between Plots
  27. Displaying Several Figures on One Page
  28. Opening Additional Graphics Windows
  29. Writing Your Plot to a File
  30. Changing Graphical Parameters

Assignment

과제명: ms23.w11.ga.covariance.exercise
제출파일명: ms23.w11.ga.covariance.exercise.group##.odc (docx)
과제내용:
아래 데이터를 다운로드 받아서 두 변인 간의 상관관계계수를 구하시오.
income.happiness.csv
income.happiness.cat.csv
데이터는 수입과 행복을 측정한 것입니다. 실제 데이터를 살펴보고 R로 읽어 온 후에 R을 이용하여 아래를 구하시오. R에서의 명령어와 아웃풋을 카피/패이스트 하여 제출하시오 (fixed-font를 사용하여).

  • 각 변인의 deviation score 값을 구하여 ds.inc 와 ds.hap 에 저장하시오.
  • 두 변인의 SP값을 (Sum of Product) 구하여 sp.dat 에 저장하시오.
  • 두 변인의 df값을 구하여 df.dat 에 저장하시오.
  • 두 변인간 covariance값을 r의 cov 명령어를 이용하여 구하여 cov.dat값에 저장하시오.
  • sp.dat / df.dat 값을 구하여 cov.cal 값에 저장하시오.
  • cov.cal 과 cov.dat 값이 같은지 비교하시오. (힌트: == 연산자를 이용하여 확인하시오)
  • 각 변인의 standard deviation 값을 구하여 sd.inc, sd.hap에 저장하시오
  • 우리가 배운 correlation값을 구하는 공식에 따라서 r 값을 구해서 r.cal 에 저장하시오.
  • R의 cor 명령어를 이용하여 correlation coefficient값을 구하여 r.dat 에 저장하시오.
  • r.cal 과 r.dat 을 비교하시오.

Week12

May 22 (월), 24 (수)

Announcement

Concepts and ideas

regression lecture note for r
동영상 Regression

  1. https://youtu.be/68gho4ubOjs : Regression 1. Intro
  2. https://youtu.be/qXSRgSh1rw0 : Regression 2. e.g. 1
  3. https://youtu.be/I8wt2W7-Iio : Regression 3. e.g. 2

chi-square test
probability
general statistics

Assignment

Week13

영상

regression_lecture_note_for_r

multiple regression lecture note for r
multiple regression

Concepts and ideas

Assignment

Week14

June 5(월), 7(수)
13주차 참조

Concepts and ideas

Assignment

Week15

June 12, 14
13주차 참조

Assignment

Week16

June 19, 21 (퀴즈일자에만 퀴즈를 보고 수업은 없음)

Final-term

  • R 관련 문제는 아웃풋을 이해하는지에 치중을 하시면 됩니다. 실제 명령어 사용 등에 대한 문제는 나오지 않습니다.
c/ms/2024/schedule.1718149623.txt.gz · Last modified: 2024/06/12 08:47 by hkimscil
Donate Powered by PHP Valid HTML5 Valid CSS Driven by DokuWiki