Standard Deviation(표준편차)는 variance(분산)값을 square root한 값을 말한다. 애초에 분산의 정도를 구하기 위해서 deviation score를 제곱한 값을 사용하였으므로 이에 다시 제곱근을 한 것이다.
$$\sigma^2=\frac{SS}{N}=\frac{SS}{N-1}=\frac{SS}{df}=\frac{\sum\limits_{i=1}^n (X_i-\mu)^2}{N-1} $$
$$\sigma=\sqrt{\sigma^2}=\sqrt{\frac{\sum\limits_{i=1}^n (X_i-\mu)^2}{N-1}} $$
$$s=\sqrt{s^2}=\sqrt{\frac{\sum\limits_{i=1}^n (X_i-\overline{X})^2}{n-1}} $$
$$s=\sqrt{s^2} $$

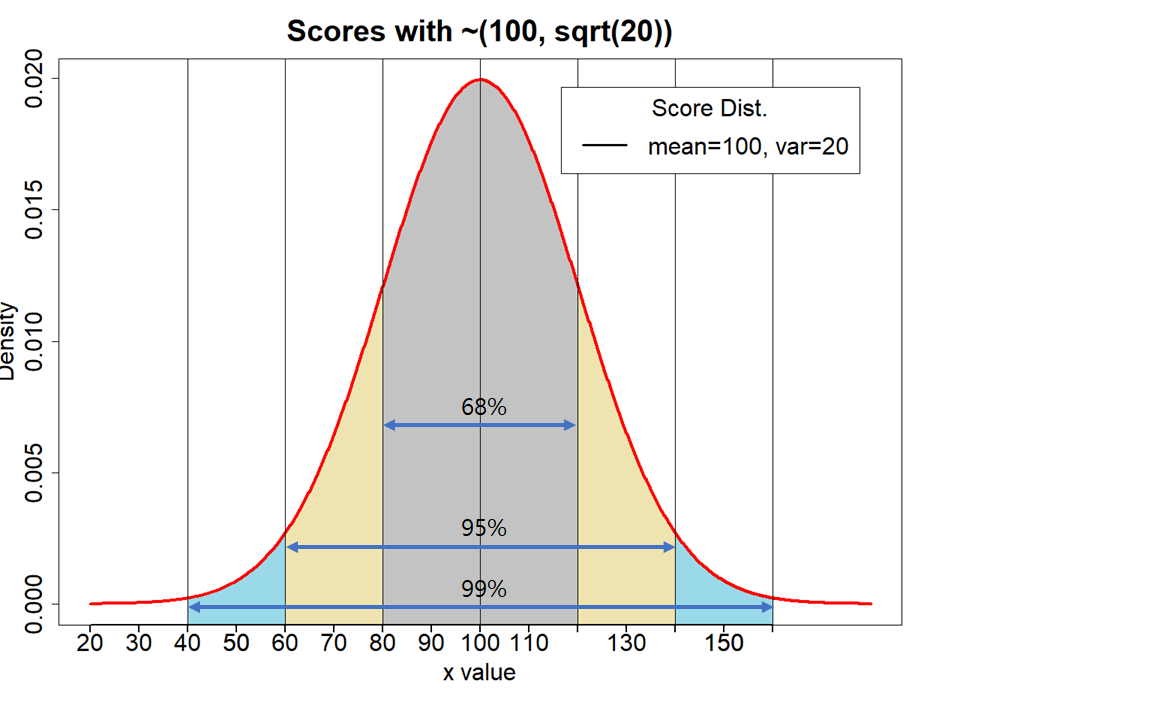
아래는 평균:100, 표준편차:20 인 변인 X 의 데이터를 그래프로 나타낸 것이다. normal distribution 정상분포의 전체 면적을 1 이라고 했을 때, 평균을 중심으로 한 standard deviation의 한 단위는 아래쪽과 위쪽 면적의 합은 전체 면적의 약 68%를 차지한다. 두 단위 아래 위쪽을 포함하는 면적은 약 95%; 그리고 세단위를 사용한 면적은 약 99%를 차지한다.

위의 그래프가 어느 집단의 IQ라는 변인을 측정한 데이타라고 가정한다면 SD 한 단위에 해당하는 80-120 사이의 사람들은 약 68%이며, 60-140은 95%, 그리고 40-160사이의 사람들은 99%를 차지한다고 생각할 수 있다. 단, IQ 점수의 분포가 정상분포곡선을 이룬다는 가정에서이다.

정확한 퍼센티지는 다음과 같다.

> pnorm(1)-pnorm(-1)  ## 68%로 줄여서 암기
[1] 0.6826895
> pnorm(2)-pnorm(-2)  ## 95%로 줄여서 암기
[1] 0.9544997
> pnorm(3)-pnorm(-3)  ## 99%로 줄여서 암기
[1] 0.9973002
> 

만약에 정확히 68%, 95%, 99% 에 해당하는 점수를 찾는다면 아래와 같이 찾을 수 있다.

> one.sd <- .68
> two.sd <- .95
> thr.sd <- .99
> 1-one.sd
[1] 0.32
> (1-one.sd)/2
[1] 0.16
> qnorm(0.16)
[1] -0.9944579
> qnorm(1-0.16)
[1] 0.9944579
> 
> 1-two.sd
[1] 0.05
> (1-two.sd)/2
[1] 0.025
> qnorm(0.025)
[1] -1.959964
> qnorm(0.975)
[1] 1.959964
> 
> 1-thr.sd
[1] 0.01
> (1-thr.sd)/2
[1] 0.005
> qnorm(0.005)
[1] -2.575829
> qnorm(1-0.005)
[1] 2.575829
> 

위의 값은 정확은 하지만 개념적으로 표준편차의 특징을 이해하는데 방해가 되는 면이 있다. 따라서 표준편차 1, 2, 3 만큼은 각각 68, 95, 99%로 기억해두는 것이 편리하다.