sampling_distribution_in_r
This is an old revision of the document!
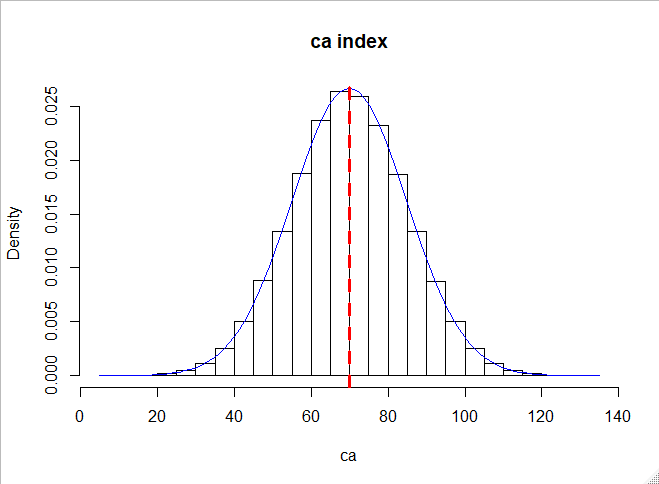
Sampling distribution in R e.g. 1
n.ca <- 100000 mean.ca <- 70 sd.ca <- 15 set.seed(2020) ca <- rnorm(n.ca, mean=mean.ca, sd=sd.ca) ca <- round(ca, 0) hist(ca, xlab="ca", main="ca index", freq=F) curve(dnorm(x, mean=mean(ca), sd=sd(ca)), add=TRUE, col="blue") abline(v=mean.ca,lwd=3,lty=2, col="red") summary(ca) mu <- round(mean(ca)) sigma <- round(sd(ca)) mu sigma
rnorm2 <- function(n,mean,sd) { mean+sd*scale(rnorm(n)) }
n.ca <- 100000
mean.ca <- 70
sd.ca <- 15
set.seed(101)
ca <- rnorm2(n.ca, mean=mean.ca, sd=sd.ca)
ca <- round(ca, 0)
hist(ca, xlab="ca", main="ca index", freq=F)
curve(dnorm(x, mean=mean(ca), sd=sd(ca)), add=TRUE, col="blue")
abline(v=mean.ca,lwd=3,lty=2, col="red")
summary(ca)
mu <- round(mean(ca))
sigma <- round(sd(ca))
mu
sigma
> summary(ca) Min. 1st Qu. Median Mean 3rd Qu. Max. 7.00 60.00 70.00 69.96 80.00 132.00 >
최소값 70
최대값 132
대강의 아이디어.
- 위의 점수가 전국 고등학교 2년생의 (모집단) 수학점수라고 가정을 하자. 그리고, 이 모집단의 수학점수 평균은 70, 표준편차는 15임을 알고 있으며 최소값과 최대값 또한 알고 있다 (각각 70, 132)
- 그런데 내가 수학을 학생들에게 (25명) 가르치는데 그 방법이 남달라서 효과가 좋다는 것을 확신한고 있다고 하자.
- 이를 증명하는데 가장 확실하게 느낄수 있는 (?) 방법은 내 학생의 점수가 위의 모집단 점수의 최대값인 132점을 넘는 것이다.
- 132점을 넘는 학생은 모집단에 속한 학생이 아니라 다른 모집단에 (나의 교육방법을 교수받은 모집단) 속한 학생이라고 생각할 수 있는 것이다.
- 내가 가르친 학생들의 평균점수가 132점을 모두 넘는다면 한 학생이 아니라 나의 집단이 (샘플이) 모집단에 속하지 않는 특별한 집단이라고 생각할 수 있다.
- 그러나 현실적으로 이렇게 판단하기에는 넘어야 할 점수가 너무 크다.
n.ajstu <- 100000
mean.ajstu <- 24
sd.ajstu <- 2
set.seed(1024)
ajstu <- rnorm2(n.ajstu, mean=mean.ajstu, sd=sd.ajstu)
mean(ajstu)
sd(ajstu)
iter <- 10000
n <- 4
means4 <- rep (NA, iter)
for(i in 1:iter){
means4[i] = mean(sample(ajstu, n))
}
n <- 25
means25 <- rep (NA, iter)
for(i in 1:iter){
means25[i] = mean(sample(ajstu, n))
}
n <- 100
means100 <- rep (NA, iter)
for(i in 1:iter){
means100[i] = mean(sample(ajstu, n))
}
n <- 400
means400 <- rep (NA, iter)
for(i in 1:iter){
means400[i] = mean(sample(ajstu, n))
}
n <- 900
means900 <- rep (NA, iter)
for(i in 1:iter){
means900[i] = mean(sample(ajstu, n))
}
n <- 1600
means1600 <- rep (NA, iter)
for(i in 1:iter){
means1600[i] = mean(sample(ajstu, n))
}
n <- 2500
means2500 <- rep (NA, iter)
for(i in 1:iter){
means2500[i] = mean(sample(ajstu, n))
}
h4 <- hist(means4)
h25 <- hist(means25)
h100 <- hist(means100)
h400 <- hist(means400)
h900 <- hist(means900)
h1600 <- hist(means1600)
h2500 <- hist(means2500)
plot(h4, ylim=c(0,3000), col="red")
plot(h25, add = T, col="blue")
plot(h100, add = T, col="green")
plot(h400, add = T, col="grey")
plot(h900, add = T, col="black")
Sampling distribution in proportion in R
pop <- rbinom(100000, size = 1, prob = 0.5)
par(mfrow=c(2,2))
iter <- 10000
n <- 5
means <- rep (NA, iter)
for(i in 1:iter){
means[i] = mean(sample(pop, n))
}
mean(means)
hist(means, xlim=c(0,1), main=n)
iter <- 10000
n <- 25
means <- rep (NA, iter)
for(i in 1:iter){
means[i] = mean(sample(pop, n))
}
mean(means)
hist(means, xlim=c(0,1), main=n)
iter <- 10000
n <- 100
means <- rep (NA, iter)
for(i in 1:iter){
means[i] = mean(sample(pop, n))
}
mean(means)
hist(means, xlim=c(0,1), main=n)
iter <- 10000
n <- 900
means <- rep (NA, iter)
for(i in 1:iter){
means[i] = mean(sample(pop, n))
}
mean(means)
sd(means)
var(means)
hist(means, xlim=c(0,1), main=n)
par(mfrow=c(1,1))
set.seed(2020)
pop <- rbinom(100000, size = 1, prob = 0.4)
par(mfrow=c(2,2))
iter <- 1000
ns <- c(25, 100, 400, 900)
l.ns <- length(ns)
for (i in 1:l.ns) {
for(k in 1:iter) {
means[k] = mean(sample(pop, ns[i]))
}
mean(means)
sd(means)
hist(means, xlim=c(0,1), main=n)
}
par(mfrow=c(1,1))
0.5가 비율인 (proportion) 모집단에 대한 여론 조사를 위해서 900명의 샘플을 취하고 이를 이용하여 모집단의 위치를 추정하자.
n <- 900 samp <- sample(pop, n) mean(samp) p <- mean(samp) q <- 1-p ser <- sqrt((p*q)/n) ser2 <- ser * 2 p - ser2 p + ser2
sampling_distribution_in_r.1710817487.txt.gz · Last modified: by hkimscil