This is an old revision of the document!
Table of Contents
Week 3 내용
SPSS
Chapter 3, Chapter 4
- SPSS
- Table 3.1 data file. for SPSS, excel format, see the below.
- Explanation: Read the textbook for yourself (Chapter 3)
- frequency distribution
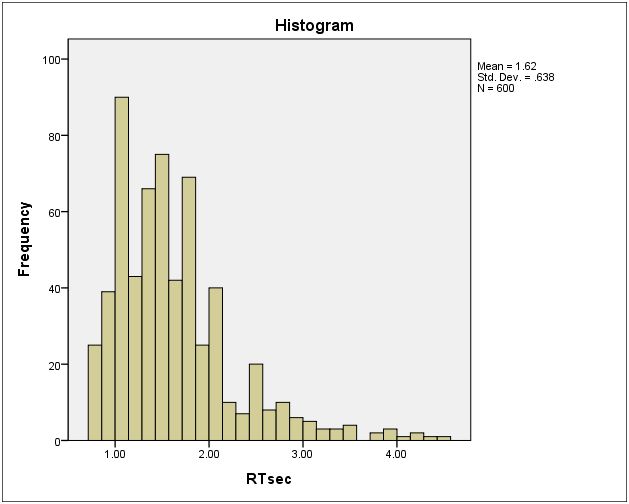
- histogram
- stem and leaf display.
- watch Spss
Central Tendency
- Central Tendency (집중경향)
- data: SPSS data file, rtsec or Excel file
Statistics RTsec N Valid 600 Missing 0 Mean 1.6245 Median 1.5300 Mode 1.33
Descriptives
StatisticStd. Error
RTsec Mean 1.6245 .02603
95% Confidence Lower 1.5734
Interval Upper 1.6756
for Mean
5% Trimmed Mean 1.5672
Median 1.5300
Variance .407
Std. Deviation .63772
Minimum .72
Maximum 4.44
Range 3.72
Interquartile Range .77
Skewness 1.465 .100
Kurtosis 2.849 .199
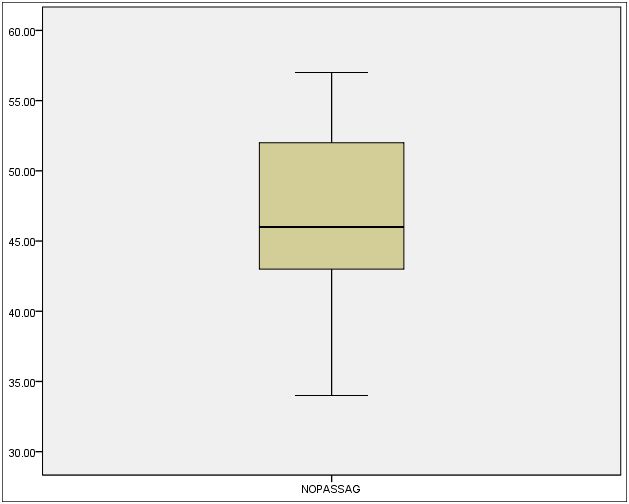
data file: ex3-1.sav 읽지 않은 지문에 대한 답을 한 학생들의 점수 (Katz, 1990).
NOPASSAG Stem-and-Leaf Plot
Frequency Stem & Leaf
1.00 3 . 4
5.00 3 . 66689
5.00 4 . 33444
7.00 4 . 6666799
5.00 5 . 01224
5.00 5 . 55577
Stem width: 10.00
Each leaf: 1 case(s)
Chapter 5
- Dispersion (variability) – 분산(변산성)
- Data file: Web site or tab5-1.sav p.86-7
- outliers: It is beyond our scope. Please just refer to it. Won't be appearing in tests.
- 평균편차
- Variance 변량
- 표본변량 $ s^2 $
- 모집단변량(전집) $ \sigma^2 $
Descriptives SET Statistic Std. Error ATTRACT 4 Mean 2.6445 .14651 95% Confidence Lower Bound 2.3379 Interval for Upper Bound 2.9511 Mean 5% Trimmed Mean 2.6483 Median 2.5950 Variance .429 Std. Deviation .65520 Minimum 1.20 Maximum 4.02 Range 2.82 Interquartile Range .82 Skewness -.001 .512 Kurtosis .438 .992 32 Mean 3.2615 .01541 95% Confidence Interval for Mean Lower Bound 3.2292 Upper Bound 3.2938 5% Trimmed Mean 3.2622 Median 3.2650 Variance .005 Std. Deviation .06892 Minimum 3.13 Maximum 3.38 Range .25 Interquartile Range .11 Skewness -.075 .512 Kurtosis -.863 .992
- Standard Deviation 표준편차
- Variance calculation formula
- variance_calculation_formula $ \displaystyle S_x^2 = \displaystyle \frac {\Sigma X^2 - \frac{(\Sigma X)^2}{N} } {N-1} $
- $ \displaystyle \sigma_x^2 = \displaystyle \frac {\Sigma X^2 - \frac{(\Sigma X)^2}{N} } {N} = \displaystyle \frac {\Sigma X^2}{N} - \frac {(\Sigma X)^2}{N^2} = \displaystyle \frac {\Sigma X^2}{N} - \bigg(\frac {\Sigma X}{N}\bigg)^2 = \displaystyle \frac {\Sigma X^2}{N} - \mu^2 $
Sampling Distribution, Standard Error
CLT에 관한 정리
우선, Expected value (기대값)와 Variance (분산)의 연산은 아래와 같이 계산될 수 있다.
X,Y 가 서로 독립적이라고 할 때:
\begin{eqnarray}
E[aX] = a E[X] \\
E[X+Y] = E[X] + E[Y] \\
Var[aX] = a^{\tiny{2}} Var[X] \\
Var[X+Y] = Var[X] + Var[Y]
\end{eqnarray}
이때, 한 샘플의 평균값을 $X$ 라고 하면, 평균들의 합인 $S_k$ 는
$$ S_{k} = X_1 + X_2 + . . . + X_k $$
와 같다.
이렇게 얻은 샘플들(k 개의)의 평균인 $ A_k $ 는,
$$ A_k = \displaystyle \frac{(X_1 + X_2 + . . . + X_k)}{k} = \frac{S_{k}}{k} $$
라고 할 수 있다.
이때,
$$
\begin{align*}
E[S_k] & = E[X_1 + X_2 + . . . +X_k] \\
& = E[X_1] + E[X_2] + . . . + E[X_k] \\
& = \mu + \mu + . . . + \mu = k * \mu \\
\end{align*}
$$
$$
\begin{align*}
Var[S_k] & = Var[X_1 + X_2 + . . . +X_k] \\
& = Var[X_1] + Var[X_2] + \dots + Var[X_k] \\
& = k * \sigma^2
\end{align*}
$$
이다.
그렇다면, $ A_k $ 에 관한 기대값과 분산값은:
$$
\begin{align*}
E[A_k] & = E[\frac{S_k}{k}] \\
& = \frac{1}{k}*E[S_k] \\
& = \frac{1}{k}*k*\mu = \mu
\end{align*}
$$
이고,
$$
\begin{align*}
Var[A_k] & = Var[\frac{S_k}{k}] \\
& = \frac{1}{k^2} Var[S_k] \\
& = \frac{1}{k^2}*k*\sigma^2 \\
& = \frac{\sigma^2}{k} \nonumber
\end{align*}
$$
라고 할 수 있다.