anova_note
Table of Contents
with 2 levels
t-test를 하는 상황 (2 sample independent t-test)
rm(list=ls())
# set.seed(101)
rnorm2 <- function(n,mean,sd){ mean+sd*scale(rnorm(n)) }
ss <- function(x) {
sum((x-mean(x))^2)
}
n.o <- 30
n.p <- 30
o <- rnorm(n.o, 100, 10)
p <- rnorm(n.p, 105, 10)
t.test(o,p, var.equal=T)
comb <- list(o = o, p = p)
op <- stack(comb)
head(op)
colnames(op)[1] <- "values"
colnames(op)[2] <- "group"
op$group <- factor(op$group)
head(op)
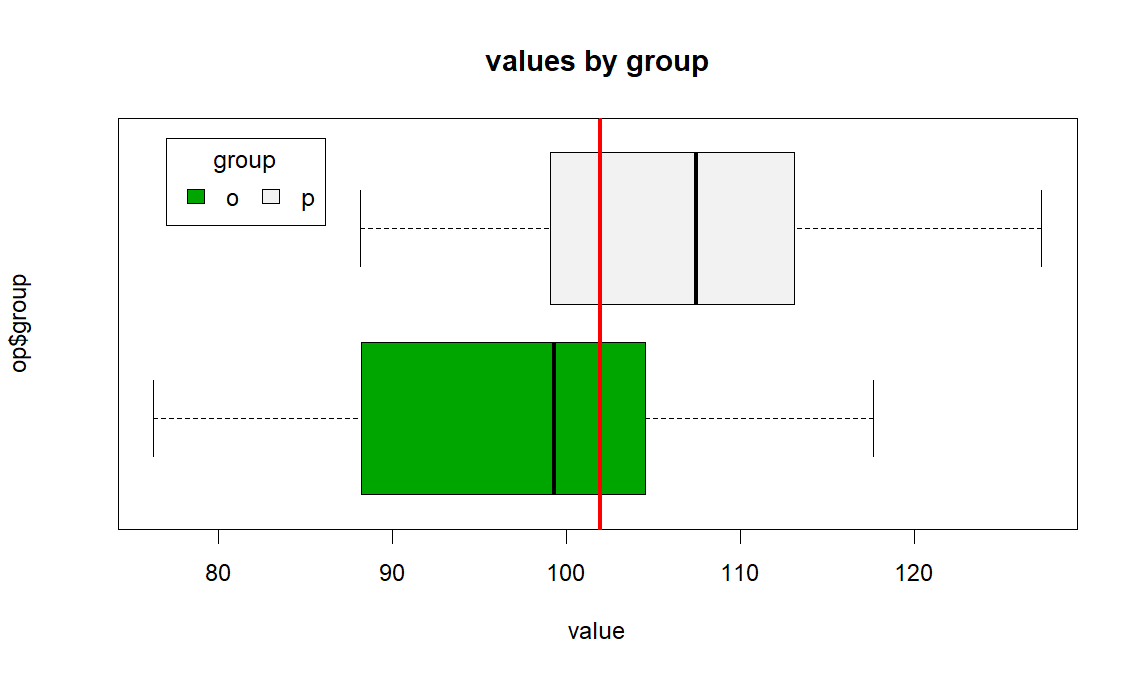
boxplot(op$values~op$group)
plot(op$values~op$group)
boxplot(op$values~op$group, main="values by group",
yaxt="n", xlab="value", horizontal=TRUE,
col=terrain.colors(2))
abline(v=mean(op$values), col="red", lwd=3)
legend("topleft", inset=.05, title="group",
c("o","p"), fill=terrain.colors(2), horiz=TRUE)
m.tot <- mean(op$values)
m.o <- mean(o)
m.p <- mean(p)
min.x <- min(op$values)
max.x <- max(op$values)
br <- seq(floor(min.x), ceiling(max.x), by = 1)
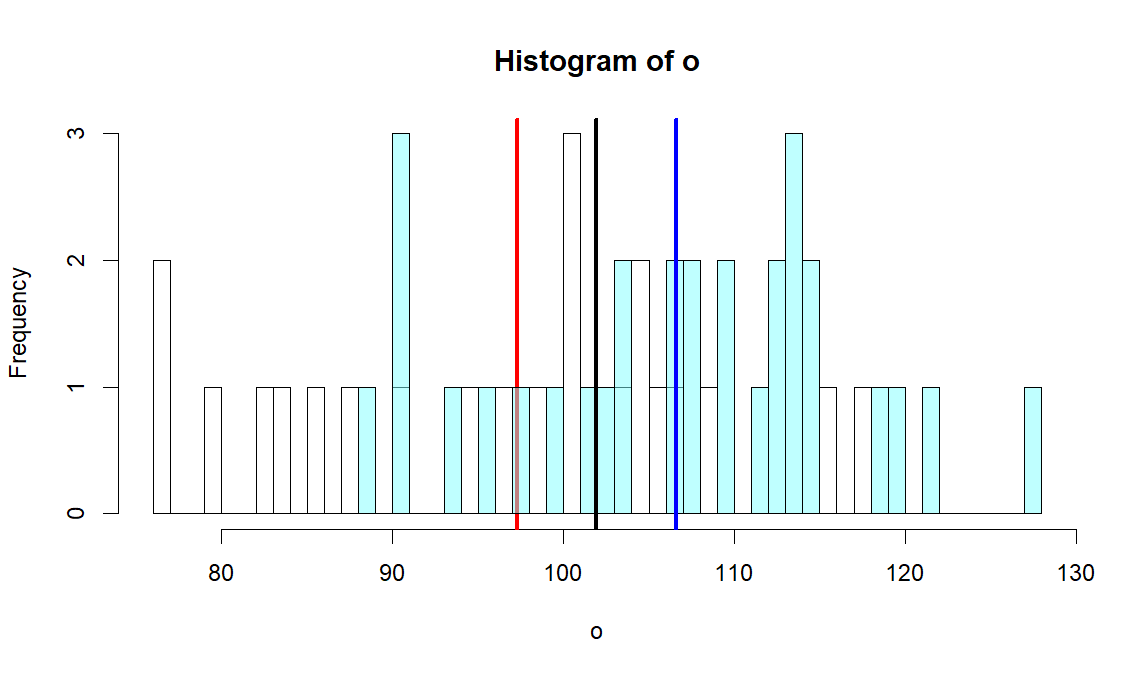
hist(o, breaks=br,
col=rgb(1,1,1,.5))
abline(v=m.o, col="red", lwd=3)
hist(p, add=T, breaks=br,
col=rgb(.5,1,1,.5))
abline(v=m.p, col="blue", lwd=3)
abline(v=m.tot, col='black', lwd=3)
ss.tot <- ss(op$values)
df.tot <- length(op$values)-1
ss.tot/df.tot
var(op$values)
ss.tot
ss.o <- ss(o)
ss.p <- ss(p)
df.o <- length(o)-1
df.p <- length(p)-1
m.tot
m.o
m.p
ss.o
ss.p
ss.bet <- length(o)*(m.tot-m.o)^2+length(p)*(m.tot-m.p)^2
ss.tot
ss.bet
ss.wit <- ss.o+ss.p
ss.wit
ss.bet+ss.wit
ss.tot
df.tot <- length(op$values)-1
df.bet <- nlevels(op$group) - 1
df.wit <- (length(o)-1)+(length(p)-1)
df.tot
df.bet
df.wit
ms.tot <- ss.tot / df.tot
ms.bet <- ss.bet / df.bet
ms.wit <- ss.wit / df.wit
f.cal <- ms.bet / ms.wit
f.cal
p.val <- pf(f.cal, df1=df.bet, df2=df.wit, lower.tail = F)
p.val
summary(aov(op$values~op$group))
t.test(o,p, var.equal = T)
diff <- m.o - m.p
ssp <- (ss.o + ss.p) / (df.o + df.p)
se <- sqrt(ssp/n.o+ssp/n.p)
t.cal <- diff/se
t.cal
p.t.cal <- pt(abs(t.cal), df=df.o+df.p, lower.tail = F)*2
p.t.cal
t.cal^2
f.cal
df.bet
df.wit
f.cal
output
> rm(list=ls())
> # set.seed(101)
> rnorm2 <- function(n,mean,sd){ mean+sd*scale(rnorm(n)) }
> ss <- function(x) {
+ sum((x-mean(x))^2)
+ }
>
> n.o <- 30
> n.p <- 30
> o <- rnorm(n.o, 100, 10)
> p <- rnorm(n.p, 105, 10)
> t.test(o,p, var.equal=T)
Two Sample t-test
data: o and p
t = -3.3581, df = 58, p-value = 0.001391
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-14.78163 -3.74076
sample estimates:
mean of x mean of y
97.31987 106.58106
> comb <- list(o = o, p = p)
> op <- stack(comb)
> head(op)
values ind
1 83.05641 o
2 108.25078 o
3 90.81559 o
4 99.74236 o
5 82.61865 o
6 85.64129 o
> colnames(op)[1] <- "values"
> colnames(op)[2] <- "group"
> op$group <- factor(op$group)
> head(op)
values group
1 83.05641 o
2 108.25078 o
3 90.81559 o
4 99.74236 o
5 82.61865 o
6 85.64129 o
> boxplot(op$values~op$group)
>
>
> plot(op$values~op$group)
> boxplot(op$values~op$group, main="values by group",
+ yaxt="n", xlab="value", horizontal=TRUE,
+ col=terrain.colors(2))
> abline(v=mean(op$values), col="red", lwd=3)
> legend("topleft", inset=.05, title="group",
+ c("o","p"), fill=terrain.colors(2), horiz=TRUE)
>
> m.tot <- mean(op$values) > m.o <- mean(o) > m.p <- mean(p) > > min.x <- min(op$values) > max.x <- max(op$values) > br <- seq(floor(min.x), ceiling(max.x), by = 1) >
> hist(o, breaks=br,
+ col=rgb(1,1,1,.5))
> abline(v=m.o, col="red", lwd=3)
> hist(p, add=T, breaks=br,
+ col=rgb(.5,1,1,.5))
> abline(v=m.p, col="blue", lwd=3)
> abline(v=m.tot, col='black', lwd=3)
>
> ss.tot <- ss(op$values)
> df.tot <- length(op$values)-1
> ss.tot/df.tot
[1] 133.9582
> var(op$values)
[1] 133.9582
> ss.tot
[1] 7903.533
>
> ss.o <- ss(o)
> ss.p <- ss(p)
> df.o <- length(o)-1
> df.p <- length(p)-1
>
> m.tot
[1] 101.9505
> m.o
[1] 97.31987
> m.p
[1] 106.5811
> ss.o
[1] 3647.085
> ss.p
[1] 2969.903
>
> ss.bet <- length(o)*(m.tot-m.o)^2+length(p)*(m.tot-m.p)^2
> ss.tot
[1] 7903.533
> ss.bet
[1] 1286.546
> ss.wit <- ss.o+ss.p
> ss.wit
[1] 6616.987
> ss.bet+ss.wit
[1] 7903.533
> ss.tot
[1] 7903.533
>
> df.tot <- length(op$values)-1
> df.bet <- nlevels(op$group) - 1
> df.wit <- (length(o)-1)+(length(p)-1)
> df.tot
[1] 59
> df.bet
[1] 1
> df.wit
[1] 58
>
> ms.tot <- ss.tot / df.tot
> ms.bet <- ss.bet / df.bet
> ms.wit <- ss.wit / df.wit
>
> f.cal <- ms.bet / ms.wit
> f.cal
[1] 11.27699
> p.val <- pf(f.cal, df1=df.bet, df2=df.wit, lower.tail = F)
> p.val
[1] 0.001390984
> summary(aov(op$values~op$group))
Df Sum Sq Mean Sq F value Pr(>F)
op$group 1 1287 1286.5 11.28 0.00139 **
Residuals 58 6617 114.1
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
> t.test(o,p, var.equal = T)
Two Sample t-test
data: o and p
t = -3.3581, df = 58, p-value = 0.001391
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-14.78163 -3.74076
sample estimates:
mean of x mean of y
97.31987 106.58106
>
> diff <- m.o - m.p
> ssp <- (ss.o + ss.p) / (df.o + df.p)
> se <- sqrt(ssp/n.o+ssp/n.p)
> t.cal <- diff/se
> t.cal
[1] -3.358122
> p.t.cal <- pt(abs(t.cal), df=df.o+df.p, lower.tail = F)*2
> p.t.cal
[1] 0.001390984
> t.cal^2
[1] 11.27699
> f.cal
[1] 11.27699
>
> df.bet
[1] 1
> df.wit
[1] 58
> f.cal
[1] 11.27699
>
>
with more than 3 levels
#
# ANOVA test with 4 levels in IV
#
rm(list=ls())
rnorm2 <- function(n,mean,sd){ mean+sd*scale(rnorm(n)) }
ss <- function(x) {
sum((x-mean(x))^2)
}
set.seed(11)
n <- 31
na <- nb <- nc <- nd <- n
mean.a <- 98
mean.b <- 99
mean.c <- 102
mean.d <- 103
A <- rnorm2(na, mean.a, sqrt(900/(na-1)))
B <- rnorm2(nb, mean.b, sqrt(900/(nb-1)))
C <- rnorm2(nc, mean.c, sqrt(900/(nc-1)))
D <- rnorm2(nd, mean.d, sqrt(900/(nd-1)))
ss(A)
var(A)
# A combined group with group A and B
# We call it group total
# we can obtain its mean, variance, ss, df, etc.
#
comb <- data.frame(A, B, C, D)
dat <- stack(comb)
head(dat)
colnames(dat)[1] <- "values"
colnames(dat)[2] <- "group"
head(dat)
m.tot <- mean(dat$values)
m.a <- mean(A)
m.b <- mean(B)
m.c <- mean(C)
m.d <- mean(D)
# 그룹 간의 차이에서 나타나는 분산
# 수업시간에 설명을 잘 들을 것
min.x <- min(dat$values)
max.x <- max(dat$values)
br <- seq(floor(min.x), ceiling(max.x), by = 1)
# Example bin width of 1
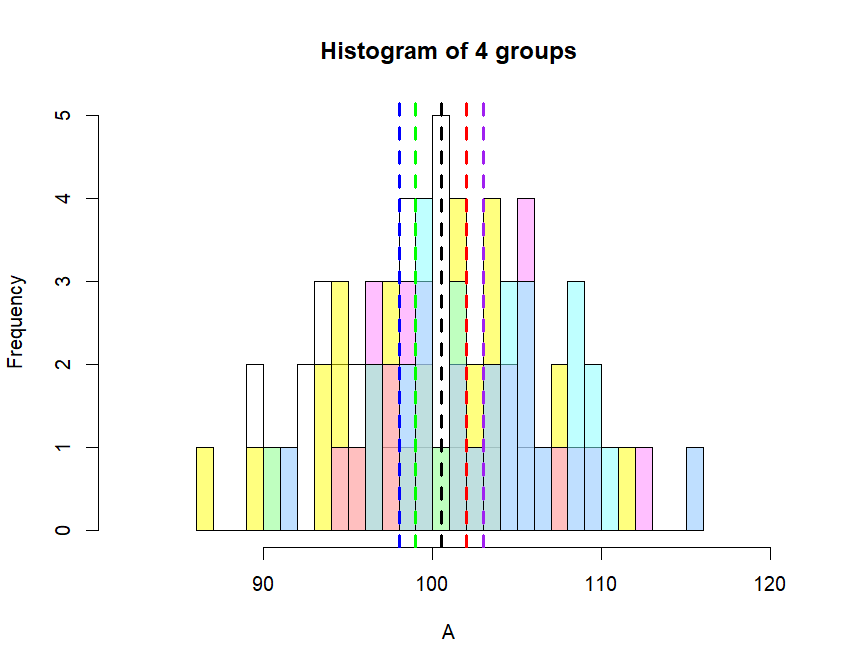
hist(A, breaks=br,
xlim = c(min.x-5, max.x+5), col=rgb(1,1,1,0.5),
main = "Histogram of 4 groups")
hist(B, breaks=br, add=T, col=rgb(1,1,0,.5))
hist(C, breaks=br, add=T, col=rgb(1,.5,1,.5))
hist(D, breaks=br, add=T, col=rgb(.5,1,1,.5))
abline(v = m.tot, lty=2, lwd=3, col="black")
abline(v = m.a, lty=2, lwd=3, col="blue")
abline(v = m.b, lty=2, lwd=3, col="green")
abline(v = m.c, lty=2, lwd=3, col="red")
abline(v = m.d, lty=2, lwd=3, col="purple")
# variance를 ms라고 부르기도 한다
var.tot <- var(dat$values)
ms.tot <- var.tot
ss.tot <- ss(dat$values)
# mean.total 에서 그룹a의 평균까지의 차이를 구한 후
# 이를 제곱하여 그룹 A 멤버의 숫자만큼 더한다 =
# 즉, SS를 구하는 방법.
# 전체평균에서 그룹평균을 뺀 것의 제곱을
# 그룹 구성원 숫자만큼 더하는 것
# 그리고 이들을 다시 모두 더하여
# ss.between에 저장
bet.ta <- (m.tot - m.a)^2 * length(A)
bet.tb <- (m.tot - m.b)^2 * length(B)
bet.tc <- (m.tot - m.c)^2 * length(C)
bet.td <- (m.tot - m.d)^2 * length(D)
ss.bet <- bet.ta +
bet.tb +
bet.tc +
bet.td
ss.a <- ss(A)
ss.b <- ss(B)
ss.c <- ss(C)
ss.d <- ss(D)
ss.wit <- ss.a+ss.b+ss.c+ss.c
ss.tot
ss.bet
ss.wit
ss.bet+ss.wit
df.tot <- length(dat$values) - 1
df.bet <- nlevels(dat$group) - 1
df.wit <- (length(A)-1) +
(length(B)-1) +
(length(C)-1) +
(length(D)-1)
df.tot
df.bet
df.wit
ms.tot <- ss.tot / df.tot
ms.bet <- ss.bet / df.bet
ms.wit <- ss.wit / df.wit
# ms.between은 그룹의 차이때문에 생긴
# 분산으로 IV 혹은 treatment 때문에 생기는
# 차이에 기인하는 분산이고
# ms.within은 각 그룹 내부에서 일어나는 분산이므로
# (variation이므로) 연구자의 관심사와는 상관이 없이
# 나타나는 random한 분산이라고 하면
# t test 때와 마찬가지로
# 그룹의 차이 / 랜덤 차이를 (에러 -> 분산은 에러라고도 했다)
# 구해볼 수 있다.
# 즉, 그룹갑분산은 사실 = diff (between groups)
# 그리고 그룹내 분산은 사실 = re
# 따라서 우리는 위 둘 간의 비율을 t test와 같이
# 살펴볼 수 있다
# 이것을 f.calculated 이라고 하고
f.cal <- ms.bet / ms.wit
f.cal
# 컴퓨터 계산이 쉬워지기 전에는 아래처럼 0.5 level
# 에서의 f값을 구한 후 이것과 계산된 f값을 비교해봤었다.
qf(.05, df1 = df.bet, df2 = df.wit, lower.tail = FALSE)
f.cal
# 위에서 f.calculated > qf값이므로
# f.calculated 값으로 영가설을 부정하고
# 연구가설을 채택하면 판단이 잘못일 확률이
# 0.05보다 작다는 것을 안다.
# 그러나 컴퓨터계산이 용이해지고서는 qf대신에
# pf를 써서 f.cal 값에 해당하는 prob. level을
# 알아본다.
# percentage of f distribution with
# df1 and df2 option
# 이는 그림의 왼쪽을 나타내므로
# 차이가 점점 커지게 되는 오른쪽을
# 계산하기 위해서는 1-x를 취한다
p.val <- pf(f.cal, df.bet, df.wit, lower.tail=F)
p.val
f.dat <- aov(dat$values~dat$group, data=dat)
summary(f.dat)
# graph 로 이해
x <- rf(50000, df1 = df.bet, df2 = df.wit)
y.max <- max(df(x, df1=df.bet, df2=df.wit))
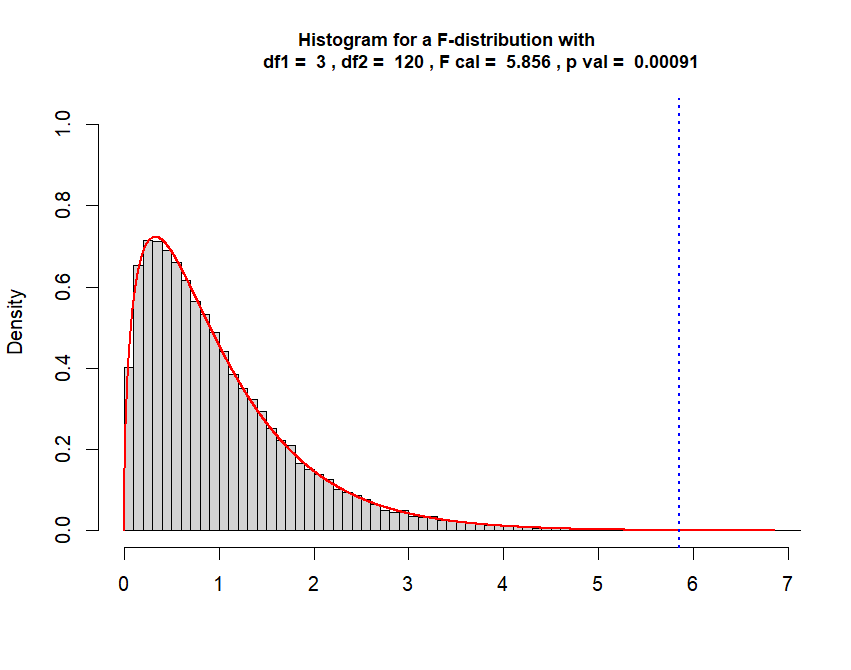
hist(x,
breaks = "Scott",
freq = FALSE,
xlim = c(0, f.cal + 1),
ylim = c(0, y.max + .3),
xlab = "",
main = paste("Histogram for a F-distribution with
df1 = ", df.bet,
", df2 = ", df.wit,
", F cal = ", round(f.cal,3),
", p val = ", round(p.val,5)),
cex.main = 0.9)
curve(df(x, df1 = df.bet, df2 = df.wit),
from = 0, to = f.cal + 1, n = 5000,
col = "red", lwd = 2,
add = T)
abline(v=f.cal, col="blue", lwd=2, lty="dotted")
f.cal
p.val
1 - p.val
# Now check this
ss.tot
ss.bet
ss.wit
ss.tot
ss.bet + ss.wit
# 한편 df는
# df.total 30 - 1
df.tot
df.bet
df.wit
df.tot
df.bet + df.wit
##################################################
a.res <- aov(values ~ group, data=dat)
a.res.sum <- summary(a.res)
a.res.sum
# 그러나 정확히 어떤 그룹에서 차이가 나는지는 판단해주지 않음
pairwise.t.test(dat$values, dat$group, p.adj = "none")
# OR
pairwise.t.test(dat$values, dat$group, p.adj = "bonf")
pairwise.t.test(dat$values, dat$group, p.adj = "holm")
# OR TukeyHSD(anova.output)
TukeyHSD(a.res)
boxplot(dat$values~dat$group)
f.cal
p.val
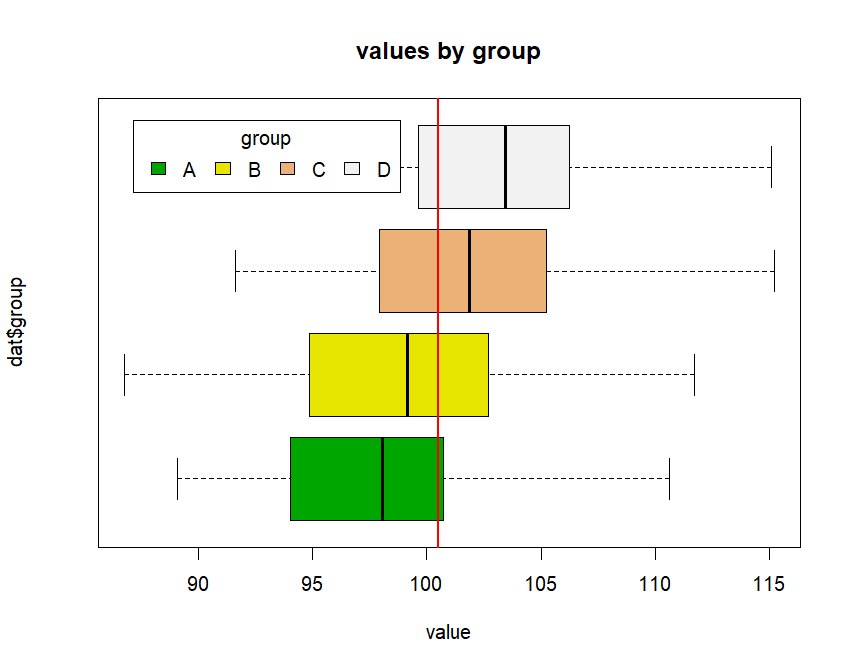
boxplot(dat$values~dat$group, main="values by group",
yaxt="n", xlab="value", horizontal=TRUE,
col=terrain.colors(4))
legend("topleft", inset=.05, title="group",
c("A","B","C", "D"), fill=terrain.colors(4), horiz=TRUE)
abline(v=mean(dat$values), col="red", lwd=2)
# how much IV explains the DV
# in terms of SS?
r.square <- ss.bet / ss.tot
eta <- r.square
eta
lm.res <- lm(dat$values~dat$group, data = dat)
summary(lm.res)
summary(a.res)
output
> #
> # ANOVA test with 4 levels in IV
> #
> rm(list=ls())
> rnorm2 <- function(n,mean,sd){ mean+sd*scale(rnorm(n)) }
> ss <- function(x) {
+ sum((x-mean(x))^2)
+ }
>
> set.seed(11)
> n <- 31
> na <- nb <- nc <- nd <- n
> mean.a <- 98
> mean.b <- 99
> mean.c <- 102
> mean.d <- 103
>
> A <- rnorm2(na, mean.a, sqrt(900/(na-1)))
> B <- rnorm2(nb, mean.b, sqrt(900/(nb-1)))
> C <- rnorm2(nc, mean.c, sqrt(900/(nc-1)))
> D <- rnorm2(nd, mean.d, sqrt(900/(nd-1)))
> ss(A)
[1] 900
> var(A)
[,1]
[1,] 30
>
> # A combined group with group A and B
> # We call it group total
> # we can obtain its mean, variance, ss, df, etc.
> #
> comb <- data.frame(A, B, C, D)
> dat <- stack(comb)
> head(dat)
values ind
1 96.21237 A
2 100.86294 A
3 89.24341 A
4 90.40224 A
5 109.53642 A
6 93.62876 A
> colnames(dat)[1] <- "values"
> colnames(dat)[2] <- "group"
> head(dat)
values group
1 96.21237 A
2 100.86294 A
3 89.24341 A
4 90.40224 A
5 109.53642 A
6 93.62876 A
>
> m.tot <- mean(dat$values)
> m.a <- mean(A)
> m.b <- mean(B)
> m.c <- mean(C)
> m.d <- mean(D)
>
> # 그룹 간의 차이에서 나타나는 분산
> # 수업시간에 설명을 잘 들을 것
> min.x <- min(dat$values)
> max.x <- max(dat$values)
> br <- seq(floor(min.x), ceiling(max.x), by = 1)
> # Example bin width of 1
>
>
> hist(A, breaks=br,
+ xlim = c(min.x-5, max.x+5), col=rgb(1,1,1,0.5),
+ main = "Histogram of 4 groups")
> hist(B, breaks=br, add=T, col=rgb(1,1,0,.5))
> hist(C, breaks=br, add=T, col=rgb(1,.5,1,.5))
> hist(D, breaks=br, add=T, col=rgb(.5,1,1,.5))
>
> abline(v = m.tot, lty=2, lwd=3, col="black")
> abline(v = m.a, lty=2, lwd=3, col="blue")
> abline(v = m.b, lty=2, lwd=3, col="green")
> abline(v = m.c, lty=2, lwd=3, col="red")
> abline(v = m.d, lty=2, lwd=3, col="purple")
>
> # variance를 ms라고 부르기도 한다
> var.tot <- var(dat$values)
> ms.tot <- var.tot
>
> ss.tot <- ss(dat$values)
> # mean.total 에서 그룹a의 평균까지의 차이를 구한 후
> # 이를 제곱하여 그룹 A 멤버의 숫자만큼 더한다 =
> # 즉, SS를 구하는 방법.
> # 전체평균에서 그룹평균을 뺀 것의 제곱을
> # 그룹 구성원 숫자만큼 더하는 것
> # 그리고 이들을 다시 모두 더하여
> # ss.between에 저장
> bet.ta <- (m.tot - m.a)^2 * length(A)
> bet.tb <- (m.tot - m.b)^2 * length(B)
> bet.tc <- (m.tot - m.c)^2 * length(C)
> bet.td <- (m.tot - m.d)^2 * length(D)
> ss.bet <- bet.ta +
+ bet.tb +
+ bet.tc +
+ bet.td
>
> ss.a <- ss(A)
> ss.b <- ss(B)
> ss.c <- ss(C)
> ss.d <- ss(D)
> ss.wit <- ss.a+ss.b+ss.c+ss.c
>
> ss.tot
[1] 4127
> ss.bet
[1] 527
> ss.wit
[1] 3600
> ss.bet+ss.wit
[1] 4127
>
> df.tot <- length(dat$values) - 1
> df.bet <- nlevels(dat$group) - 1
> df.wit <- (length(A)-1) +
+ (length(B)-1) +
+ (length(C)-1) +
+ (length(D)-1)
> df.tot
[1] 123
> df.bet
[1] 3
> df.wit
[1] 120
>
> ms.tot <- ss.tot / df.tot
> ms.bet <- ss.bet / df.bet
> ms.wit <- ss.wit / df.wit
>
> # ms.between은 그룹의 차이때문에 생긴
> # 분산으로 IV 혹은 treatment 때문에 생기는
> # 차이에 기인하는 분산이고
>
> # ms.within은 각 그룹 내부에서 일어나는 분산이므로
> # (variation이므로) 연구자의 관심사와는 상관이 없이
> # 나타나는 random한 분산이라고 하면
>
> # t test 때와 마찬가지로
> # 그룹의 차이 / 랜덤 차이를 (에러 -> 분산은 에러라고도 했다)
> # 구해볼 수 있다.
>
> # 즉, 그룹갑분산은 사실 = diff (between groups)
> # 그리고 그룹내 분산은 사실 = re
> # 따라서 우리는 위 둘 간의 비율을 t test와 같이
> # 살펴볼 수 있다
> # 이것을 f.calculated 이라고 하고
>
> f.cal <- ms.bet / ms.wit
> f.cal
[1] 5.855556
>
> # 컴퓨터 계산이 쉬워지기 전에는 아래처럼 0.5 level
> # 에서의 f값을 구한 후 이것과 계산된 f값을 비교해봤었다.
> qf(.05, df1 = df.bet, df2 = df.wit, lower.tail = FALSE)
[1] 2.680168
> f.cal
[1] 5.855556
> # 위에서 f.calculated > qf값이므로
> # f.calculated 값으로 영가설을 부정하고
> # 연구가설을 채택하면 판단이 잘못일 확률이
> # 0.05보다 작다는 것을 안다.
> # 그러나 컴퓨터계산이 용이해지고서는 qf대신에
> # pf를 써서 f.cal 값에 해당하는 prob. level을
> # 알아본다.
>
> # percentage of f distribution with
> # df1 and df2 option
> # 이는 그림의 왼쪽을 나타내므로
> # 차이가 점점 커지게 되는 오른쪽을
> # 계산하기 위해서는 1-x를 취한다
>
> p.val <- pf(f.cal, df.bet, df.wit, lower.tail=F)
> p.val
[1] 0.0009119191
>
> f.dat <- aov(dat$values~dat$group, data=dat)
> summary(f.dat)
Df Sum Sq Mean Sq F value Pr(>F)
dat$group 3 527 175.7 5.856 0.000912 ***
Residuals 120 3600 30.0
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
>
> # graph 로 이해
> x <- rf(50000, df1 = df.bet, df2 = df.wit)
> y.max <- max(df(x, df1=df.bet, df2=df.wit))
>
> hist(x,
+ breaks = "Scott",
+ freq = FALSE,
+ xlim = c(0, f.cal + 1),
+ ylim = c(0, y.max + .3),
+ xlab = "",
+ main = paste("Histogram for a F-distribution with
+ df1 = ", df.bet,
+ ", df2 = ", df.wit,
+ ", F cal = ", round(f.cal,3),
+ ", p val = ", round(p.val,5)),
+ cex.main = 0.9)
> curve(df(x, df1 = df.bet, df2 = df.wit),
+ from = 0, to = f.cal + 1, n = 5000,
+ col = "red", lwd = 2,
+ add = T)
> abline(v=f.cal, col="blue", lwd=2, lty="dotted")
>
> f.cal
[1] 5.855556
> p.val
[1] 0.0009119191
> 1 - p.val
[1] 0.9990881
>
> # Now check this
> ss.tot
[1] 4127
> ss.bet
[1] 527
> ss.wit
[1] 3600
> ss.tot
[1] 4127
> ss.bet + ss.wit
[1] 4127
>
> # 한편 df는
> # df.total 30 - 1
> df.tot
[1] 123
> df.bet
[1] 3
> df.wit
[1] 120
> df.tot
[1] 123
> df.bet + df.wit
[1] 123
>
>
>
> ##################################################
> a.res <- aov(values ~ group, data=dat)
> a.res.sum <- summary(a.res)
> a.res.sum
Df Sum Sq Mean Sq F value Pr(>F)
group 3 527 175.7 5.856 0.000912 ***
Residuals 120 3600 30.0
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
> # 그러나 정확히 어떤 그룹에서 차이가 나는지는 판단해주지 않음
> pairwise.t.test(dat$values, dat$group, p.adj = "none")
Pairwise comparisons using t tests with pooled SD
data: dat$values and dat$group
A B C
B 0.47366 - -
C 0.00478 0.03305 -
D 0.00047 0.00478 0.47366
P value adjustment method: none
> # OR
> pairwise.t.test(dat$values, dat$group, p.adj = "bonf")
Pairwise comparisons using t tests with pooled SD
data: dat$values and dat$group
A B C
B 1.0000 - -
C 0.0287 0.1983 -
D 0.0028 0.0287 1.0000
P value adjustment method: bonferroni
> pairwise.t.test(dat$values, dat$group, p.adj = "holm")
Pairwise comparisons using t tests with pooled SD
data: dat$values and dat$group
A B C
B 0.9473 - -
C 0.0239 0.0991 -
D 0.0028 0.0239 0.9473
P value adjustment method: holm
>
> # OR TukeyHSD(anova.output)
> TukeyHSD(a.res)
Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = values ~ group, data = dat)
$group
diff lwr upr p adj
B-A 1 -2.6246725 4.624673 0.8894474
C-A 4 0.3753275 7.624673 0.0243602
D-A 5 1.3753275 8.624673 0.0026368
C-B 3 -0.6246725 6.624673 0.1415754
D-B 4 0.3753275 7.624673 0.0243602
D-C 1 -2.6246725 4.624673 0.8894474
>
> boxplot(dat$values~dat$group)
>
> f.cal
[1] 5.855556
> p.val
[1] 0.0009119191
>
> boxplot(dat$values~dat$group, main="values by group",
+ yaxt="n", xlab="value", horizontal=TRUE,
+ col=terrain.colors(4))
> legend("topleft", inset=.05, title="group",
+ c("A","B","C", "D"), fill=terrain.colors(4), horiz=TRUE)
> abline(v=mean(dat$values), col="red", lwd=2)
>
>
> # how much IV explains the DV
> # in terms of SS?
> r.square <- ss.bet / ss.tot
> eta <- r.square
> eta
[1] 0.1276957
> lm.res <- lm(dat$values~dat$group, data = dat)
> summary(lm.res)
Call:
lm(formula = dat$values ~ dat$group, data = dat)
Residuals:
Min 1Q Median 3Q Max
-12.9462 -3.7708 0.0944 3.1225 13.2340
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 98.0000 0.9837 99.620 < 2e-16 ***
dat$groupB 1.0000 1.3912 0.719 0.473664
dat$groupC 4.0000 1.3912 2.875 0.004779 **
dat$groupD 5.0000 1.3912 3.594 0.000474 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 5.477 on 120 degrees of freedom
Multiple R-squared: 0.1277, Adjusted R-squared: 0.1059
F-statistic: 5.856 on 3 and 120 DF, p-value: 0.0009119
> summary(a.res)
Df Sum Sq Mean Sq F value Pr(>F)
group 3 527 175.7 5.856 0.000912 ***
Residuals 120 3600 30.0
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
>
>
>
anova_note.txt · Last modified: by hkimscil