> 
> rm(list=ls())
> 
> rnorm2 <- function(n,mean,sd){ 
+   mean+sd*scale(rnorm(n)) 
+ }
> 
> set.seed(1111)
> n.p <- 10000
> m.p <- 100
> sd.p <- 10
> p1 <- rnorm2(n.p, m.p, sd.p)
> m.p1 <- mean(p1)
> sd.p1 <- sd(p1)
> 
> p2 <- rnorm2(n.p, m.p+5, sd.p)
> m.p2 <- mean(p2)
> sd.p2 <- sd(p2)
> 
>

…………………….

> n.s <- 40
> se.z1 <- c(sqrt(var(p1)/n.s))
> se.z2 <- c(sqrt(var(p2)/n.s))
> 
> x.p1 <- seq(mean(p1)-5*se.z1, 
+                 mean(p2)+5*se.z1, 
+                 length.out = 500)
> x.p2 <- seq(mean(p2)-5*se.z1, 
+             mean(p2)+5*se.z1, 
+             length.out = 500)
> 
> # Calculate the probability 
> # density for a normal distribution
> y.p1 <- dnorm(x.p1, mean(p1), se.z1)
> y.p2 <- dnorm(x.p2, mean(p2), se.z2)
> 
> # Plot the theoretical PDF
> plot(x.p1, y.p1, type = "l", 
+      lwd=3, 
+      main = "Sample means from p1 and p2 (imaginary)",
+      xlab = "Value", ylab = "Density")
> lines(x.p2, y.p2, lty=2, lwd=3)
> 
> 
> m.p1 <- mean(p1)
> se1 <- c(m.p1-se.z1, m.p1+se.z1)
> se2 <- c(m.p1-2*se.z1, m.p1+2*se.z1)
> se3 <- c(m.p1-3*se.z1, m.p1+3*se.z1)
> abline(v=c(m.p1,se1,se2,se3), 
+        col=c('black', 'orange', 'orange', 
+              'green', 'green', 
+              'blue', 'blue'), 
+        lwd=1)
> 
> treated.s <- sample(p2, n.s)
> m.treated.s <- mean(treated.s)
> m.treated.s 
[1] 102.4867
> # m.treated.s <- 103.1605 
> # set.seed(101)에서 얻은 treated.s 점수를 유지
> abline(v=m.treated.s, col='red', lwd=2)
> 

…………………….

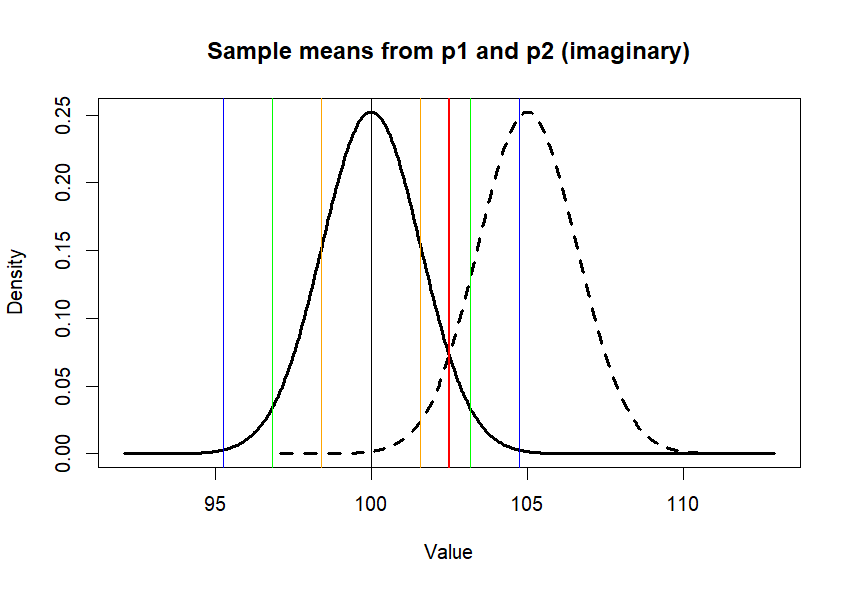
검은색 실선 (distribution of means)
검은색 선 (mean of p1, 100)
노란색 (+- se)
연두색 (+- 2se)
파란색 (+- 3se)

검은색 점선 (distribution of means from p2, 평균 = 105): 약을 먹고 머리가 좋아진 모집단. 105로 5만큼 좋아졌다고 가정한 것. 사실, 머리가 좋아지는 약을 개발했다면 그 약을 먹은 모집단의 파라미터는 알수가 없다. 단지 105라고 가정한 것이다.
붉은색 (a sample from p2) = 102.4867 : 이 점수는 105점 집단에서 (p2) 나온 n=40의 샘플. 이 샘플은 p2에서 추출되었기에 105점의 모집단에 속한 샘플이다.

> se.z1
[1] 1.581139
> 
> diff <- m.treated.s-mean(p1)
> diff/se.z1
[1] 1.572729
> 
> # usual way - using sample's variance 
> # instead of p1's variance to get
> # standard error value
> se.s <- sqrt(var(treated.s)/n.s)
> se.s
[1] 1.567184
> diff/se.s
[1] 1.586733
> 
> pt(diff/se.s, df=n.s-1, 
+    lower.tail = F) * 2
[1] 0.1206489
> t.test(treated.s, mu=m.p1, var.equal = T)

	One Sample t-test

data:  treated.s
t = 1.5867, df = 39, p-value = 0.1206
alternative hypothesis: true mean is not equal to 100
95 percent confidence interval:
  99.31677 105.65663
sample estimates:
mean of x 
 102.4867 
>
> 

…………………….
그러나, 이 샘플의 평균이 p1에 속한다고 하고, 이 평균값이 나올 확률을 알아보려면

pnorm(m.treated.s, mean=m.p1, sd=se.z, lower.tail=F) * 2

일 것이다. 그리고,

이 빨간 선에 해당하는 점수 m.treated.s의 표준점수는 (이 점수가 p1에 속한다고 가정했을 때)
\begin{eqnarray*} & & \dfrac{(\text{m.treated.s} - \text{m.p1})} {se.z} \\ & & = \dfrac{\text{diff}} {\text{se.z}} \\ & & = 1.572729 \end{eqnarray*}
우리는 이 점수가 +- 2 점을 넘는가를 보려고 한것이다. 그러나, 2점을 넘지 못하기에 이 점수가 p1에서 나올만 한 점수라고 인정할 수 밖에 없다. 즉, 영가설을 부정하려고 한것이 실패하여, 원래의 연구가설을 검증을 하지 못하게 된다. 즉, 약의 효과가 있다고 주장할 수 없게 된다. 그러나, 우리가 m.treated.s 값을 얻은 경로를 보면 이 값은 분명 p2에서 나왔으므로 연구가설 검증에 성공했어야 했다. 따라서 우리가 내린 판단은 잘못된 것이라고 하겠다. 이런 잘못된 판단을 Type I Error라고 한다.