see hypothesis testing in r space
and hypothesis testing

rm(list=ls())

rnorm2 <- function(n,mean,sd){ 
  mean+sd*scale(rnorm(n)) 
}

set.seed(1111)
n.p <- 10000
m.p <- 100
sd.p <- 10
p1 <- rnorm2(n.p, m.p, sd.p)
m.p1 <- mean(p1)
sd.p1 <- sd(p1)

p2 <- rnorm2(n.p, m.p+5, sd.p)
m.p2 <- mean(p2)
sd.p2 <- sd(p2)

n.s <- 40
se.z1 <- c(sqrt(var(p1)/n.s))
se.z2 <- c(sqrt(var(p2)/n.s))

x.p1 <- seq(mean(p1)-5*se.z1, 
                mean(p2)+5*se.z1, 
                length.out = 500)
x.p2 <- seq(mean(p2)-5*se.z1, 
            mean(p2)+5*se.z1, 
            length.out = 500)

# Calculate the probability 
# density for a normal distribution
y.p1 <- dnorm(x.p1, mean(p1), se.z1)
y.p2 <- dnorm(x.p2, mean(p2), se.z2)

# Plot the theoretical PDF
plot(x.p1, y.p1, type = "l", 
     lwd=3, 
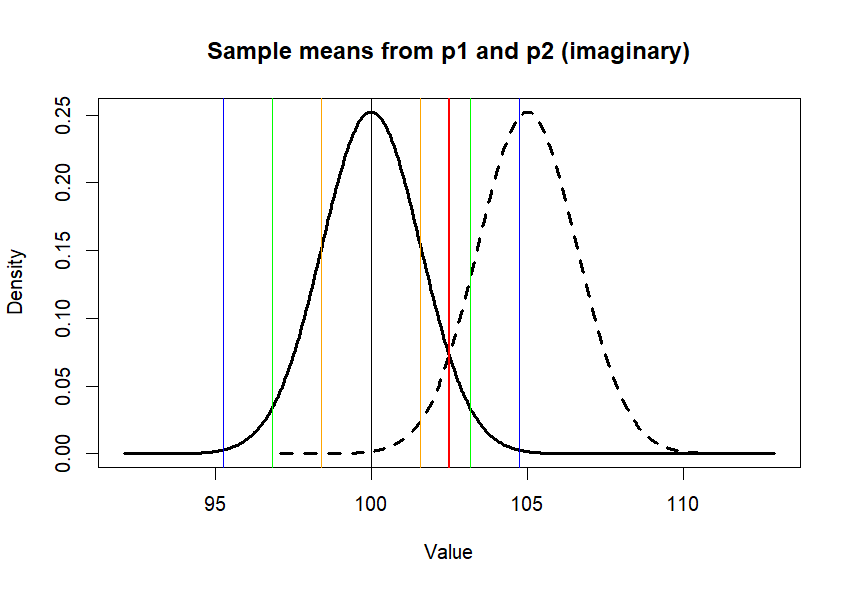
     main = "Sample means from p1 and p2 (imaginary)",
     xlab = "Value", ylab = "Density")
lines(x.p2, y.p2, lty=2, lwd=3)


m.p1 <- mean(p1)
se1 <- c(m.p1-se.z1, m.p1+se.z1)
se2 <- c(m.p1-2*se.z1, m.p1+2*se.z1)
se3 <- c(m.p1-3*se.z1, m.p1+3*se.z1)
abline(v=c(m.p1,se1,se2,se3), 
       col=c('black', 'orange', 'orange', 
             'green', 'green', 
             'blue', 'blue'), 
       lwd=1)

treated.s <- sample(p2, n.s)
m.treated.s <- mean(treated.s)
# m.treated.s <- 103.1605 # set.seed(101)에서 얻은 treated.s 점수를 유지
abline(v=m.treated.s, col='red', lwd=2)

se.z1

diff <- m.treated.s-mean(p1)
diff/se.z1

# usual way - using sample's variance 
# instead of p1's variance to get
# standard error value
se.s <- sqrt(var(treated.s)/n.s)
se.s
diff/se.s

pt(diff/se.s, df=n.s-1, 
   lower.tail = F) * 2
t.test(treated.s, mu=m.p1, var.equal = T)

> 
> rm(list=ls())
> 
> rnorm2 <- function(n,mean,sd){ 
+   mean+sd*scale(rnorm(n)) 
+ }
> 
> set.seed(1111)
> n.p <- 10000
> m.p <- 100
> sd.p <- 10
> p1 <- rnorm2(n.p, m.p, sd.p)
> m.p1 <- mean(p1)
> sd.p1 <- sd(p1)
> 
> p2 <- rnorm2(n.p, m.p+5, sd.p)
> m.p2 <- mean(p2)
> sd.p2 <- sd(p2)
> 
> n.s <- 40
> se.z1 <- c(sqrt(var(p1)/n.s))
> se.z2 <- c(sqrt(var(p2)/n.s))
> 
> x.p1 <- seq(mean(p1)-5*se.z1, 
+                 mean(p2)+5*se.z1, 
+                 length.out = 500)
> x.p2 <- seq(mean(p2)-5*se.z1, 
+             mean(p2)+5*se.z1, 
+             length.out = 500)
> 
> # Calculate the probability 
> # density for a normal distribution
> y.p1 <- dnorm(x.p1, mean(p1), se.z1)
> y.p2 <- dnorm(x.p2, mean(p2), se.z2)
> 
> # Plot the theoretical PDF
> plot(x.p1, y.p1, type = "l", 
+      lwd=3, 
+      main = "Sample means from p1 and p2 (imaginary)",
+      xlab = "Value", ylab = "Density")
> lines(x.p2, y.p2, lty=2, lwd=3)
> 
> 
> m.p1 <- mean(p1)
> se1 <- c(m.p1-se.z1, m.p1+se.z1)
> se2 <- c(m.p1-2*se.z1, m.p1+2*se.z1)
> se3 <- c(m.p1-3*se.z1, m.p1+3*se.z1)
> abline(v=c(m.p1,se1,se2,se3), 
+        col=c('black', 'orange', 'orange', 
+              'green', 'green', 
+              'blue', 'blue'), 
+        lwd=1)
> 
> treated.s <- sample(p2, n.s)
> m.treated.s <- mean(treated.s)
> # m.treated.s <- 103.1605 # set.seed(101)에서 얻은 treated.s 점수를 유지
> abline(v=m.treated.s, col='red', lwd=2)
> 
> se.z1
[1] 1.581139
> 
> diff <- m.treated.s-mean(p1)
> diff/se.z1
[1] 1.572729
> 
> # usual way - using sample's variance 
> # instead of p1's variance to get
> # standard error value
> se.s <- sqrt(var(treated.s)/n.s)
> se.s
[1] 1.567184
> diff/se.s
[1] 1.586733
> 
> pt(diff/se.s, df=n.s-1, 
+    lower.tail = F) * 2
[1] 0.1206489
> t.test(treated.s, mu=m.p1, var.equal = T)

	One Sample t-test

data:  treated.s
t = 1.5867, df = 39, p-value = 0.1206
alternative hypothesis: true mean is not equal to 100
95 percent confidence interval:
  99.31677 105.65663
sample estimates:
mean of x 
 102.4867 

> 

cm.treated.s = 102.4867 -- > RED LINE
This red line came from p2, whose mean is different from p1's. We know that p2's mean is 5 greater than p1's (100). And red line (mean of a sample from p2, whose sample size (s.size) 100. So the truth is that we should deny null hypothesis, and accept the alternative (research) one. But, because of the value, m.treated.s we could not. We failed to find out the truth (ERROR). This kind of error is called Type I Error.