see hypothesis testing in r space
and hypothesis testing

rm(list=ls())

rnorm2 <- function(n,mean,sd){ 
  mean+sd*scale(rnorm(n)) 
}

set.seed(1111)
n.p <- 10000
m.p <- 100
sd.p <- 10
p1 <- rnorm2(n.p, m.p, sd.p)
m.p1 <- mean(p1)
sd.p1 <- sd(p1)

p2 <- rnorm2(n.p, m.p+5, sd.p)
m.p2 <- mean(p2)
sd.p2 <- sd(p2)

n.s <- 40
se.z1 <- c(sqrt(var(p1)/n.s))
se.z2 <- c(sqrt(var(p2)/n.s))

x.p1 <- seq(mean(p1)-5*se.z1, 
                mean(p2)+5*se.z1, 
                length.out = 500)
x.p2 <- seq(mean(p2)-5*se.z1, 
            mean(p2)+5*se.z1, 
            length.out = 500)

# Calculate the probability 
# density for a normal distribution
y.p1 <- dnorm(x.p1, mean(p1), se.z1)
y.p2 <- dnorm(x.p2, mean(p2), se.z2)

# Plot the theoretical PDF
plot(x.p1, y.p1, type = "l", 
     lwd=3, 
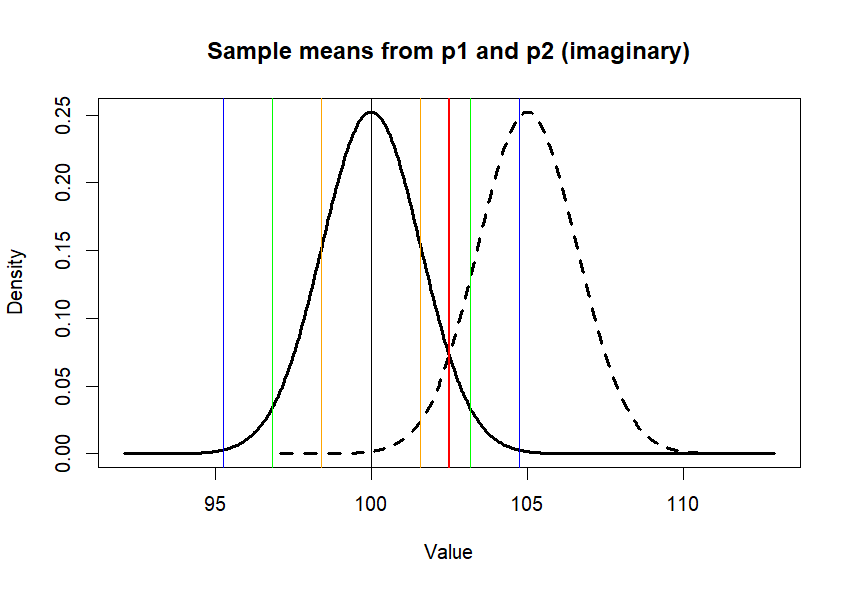
     main = "Sample means from p1 and p2 (imaginary)",
     xlab = "Value", ylab = "Density")
lines(x.p2, y.p2, lty=2, lwd=3)


m.p1 <- mean(p1)
se1 <- c(m.p1-se.z1, m.p1+se.z1)
se2 <- c(m.p1-2*se.z1, m.p1+2*se.z1)
se3 <- c(m.p1-3*se.z1, m.p1+3*se.z1)
abline(v=c(m.p1,se1,se2,se3), 
       col=c('black', 'orange', 'orange', 
             'green', 'green', 
             'blue', 'blue'), 
       lwd=1)

treated.s <- sample(p2, n.s)
m.treated.s <- mean(treated.s)
# m.treated.s <- 103.1605 # set.seed(101)에서 얻은 treated.s 점수를 유지
abline(v=m.treated.s, col='red', lwd=2)

se.z1

diff <- m.treated.s-mean(p1)
diff/se.z1

# usual way - using sample's variance 
# instead of p1's variance to get
# standard error value
se.s <- sqrt(var(treated.s)/n.s)
se.s
diff/se.s

pt(diff/se.s, df=n.s-1, 
   lower.tail = F) * 2
t.test(treated.s, mu=m.p1, var.equal = T)

> 
> rm(list=ls())
> 
> rnorm2 <- function(n,mean,sd){ 
+   mean+sd*scale(rnorm(n)) 
+ }
> 
> set.seed(1111)
> n.p <- 10000
> m.p <- 100
> sd.p <- 10
> p1 <- rnorm2(n.p, m.p, sd.p)
> m.p1 <- mean(p1)
> sd.p1 <- sd(p1)
> 
> p2 <- rnorm2(n.p, m.p+5, sd.p)
> m.p2 <- mean(p2)
> sd.p2 <- sd(p2)
> 
> n.s <- 40
> se.z1 <- c(sqrt(var(p1)/n.s))
> se.z2 <- c(sqrt(var(p2)/n.s))
> 
> x.p1 <- seq(mean(p1)-5*se.z1, 
+                 mean(p2)+5*se.z1, 
+                 length.out = 500)
> x.p2 <- seq(mean(p2)-5*se.z1, 
+             mean(p2)+5*se.z1, 
+             length.out = 500)
> 
> # Calculate the probability 
> # density for a normal distribution
> y.p1 <- dnorm(x.p1, mean(p1), se.z1)
> y.p2 <- dnorm(x.p2, mean(p2), se.z2)
> 
> # Plot the theoretical PDF
> plot(x.p1, y.p1, type = "l", 
+      lwd=3, 
+      main = "Sample means from p1 and p2 (imaginary)",
+      xlab = "Value", ylab = "Density")
> lines(x.p2, y.p2, lty=2, lwd=3)
> 
> 
> m.p1 <- mean(p1)
> se1 <- c(m.p1-se.z1, m.p1+se.z1)
> se2 <- c(m.p1-2*se.z1, m.p1+2*se.z1)
> se3 <- c(m.p1-3*se.z1, m.p1+3*se.z1)
> abline(v=c(m.p1,se1,se2,se3), 
+        col=c('black', 'orange', 'orange', 
+              'green', 'green', 
+              'blue', 'blue'), 
+        lwd=1)
> 
> treated.s <- sample(p2, n.s)
> m.treated.s <- mean(treated.s)
> # m.treated.s <- 103.1605 # set.seed(101)에서 얻은 treated.s 점수를 유지
> abline(v=m.treated.s, col='red', lwd=2)
> 
> se.z1
[1] 1.581139
> 
> diff <- m.treated.s-mean(p1)
> diff/se.z1
[1] 1.572729
> 
> # usual way - using sample's variance 
> # instead of p1's variance to get
> # standard error value
> se.s <- sqrt(var(treated.s)/n.s)
> se.s
[1] 1.567184
> diff/se.s
[1] 1.586733
> 
> pt(diff/se.s, df=n.s-1, 
+    lower.tail = F) * 2
[1] 0.1206489
> t.test(treated.s, mu=m.p1, var.equal = T)

	One Sample t-test

data:  treated.s
t = 1.5867, df = 39, p-value = 0.1206
alternative hypothesis: true mean is not equal to 100
95 percent confidence interval:
  99.31677 105.65663
sample estimates:
mean of x 
 102.4867 

> 

cm.treated.s = 102.4867 -- >
→ –>