multicolinearity
This is an old revision of the document!
Multi-colinearity
> cps <- read.csv("http://commres.net/wiki/_media/cps_85_wages.csv", header = T, sep = "\t")
> str(cps) 'data.frame': 534 obs. of 11 variables: $ education : int 8 9 12 12 12 13 10 12 16 12 ... $ south : int 0 0 0 0 0 0 1 0 0 0 ... $ sex : int 1 1 0 0 0 0 0 0 0 0 ... $ experience: int 21 42 1 4 17 9 27 9 11 9 ... $ union : int 0 0 0 0 0 1 0 0 0 0 ... $ wage : num 5.1 4.95 6.67 4 7.5 ... $ age : int 35 57 19 22 35 28 43 27 33 27 ... $ race : int 2 3 3 3 3 3 3 3 3 3 ... $ occupation: int 6 6 6 6 6 6 6 6 6 6 ... $ sector : int 1 1 1 0 0 0 0 0 1 0 ... $ marr : int 1 1 0 0 1 0 0 0 1 0 ... > head(cps) > head(cps) education south sex experience union wage age race occupation sector marr 1 8 0 1 21 0 5.10 35 2 6 1 1 2 9 0 1 42 0 4.95 57 3 6 1 1 3 12 0 0 1 0 6.67 19 3 6 1 0 4 12 0 0 4 0 4.00 22 3 6 0 0 5 12 0 0 17 0 7.50 35 3 6 0 1 6 13 0 0 9 1 13.07 28 3 6 0 0
> lm1 = lm(log(cps$wage) ~., data = cps)
> summary(lm1)
Call:
lm(formula = log(cps$wage) ~ ., data = cps)
Residuals:
Min 1Q Median 3Q Max
-2.16246 -0.29163 -0.00469 0.29981 1.98248
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.078596 0.687514 1.569 0.117291
education 0.179366 0.110756 1.619 0.105949
south -0.102360 0.042823 -2.390 0.017187 *
sex -0.221997 0.039907 -5.563 4.24e-08 ***
experience 0.095822 0.110799 0.865 0.387531
union 0.200483 0.052475 3.821 0.000149 ***
age -0.085444 0.110730 -0.772 0.440671
race 0.050406 0.028531 1.767 0.077865 .
occupation -0.007417 0.013109 -0.566 0.571761
sector 0.091458 0.038736 2.361 0.018589 *
marr 0.076611 0.041931 1.827 0.068259 .
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.4398 on 523 degrees of freedom
Multiple R-squared: 0.3185, Adjusted R-squared: 0.3054
F-statistic: 24.44 on 10 and 523 DF, p-value: < 2.2e-16
plot(lm1)
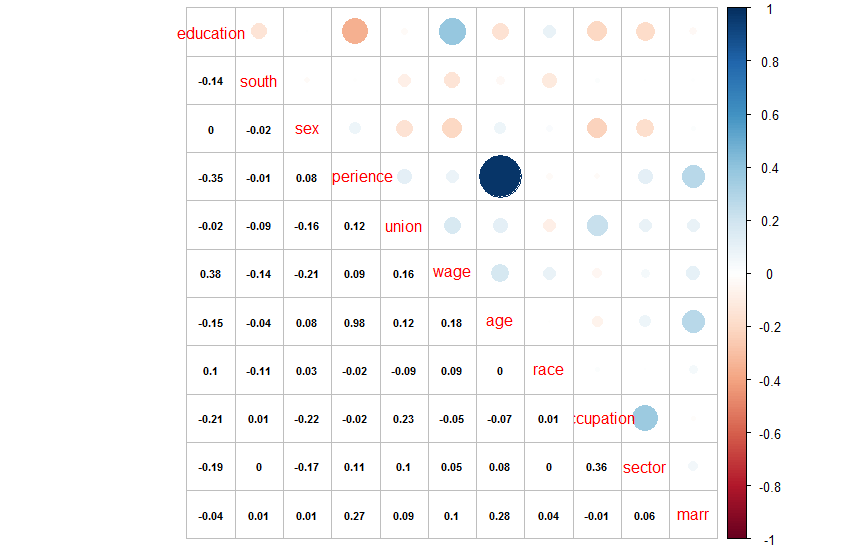
> library(corrplot) > cps.cor = cor(cps) > corrplot.mixed(cps.cor, lower.col = "black", number.cex = .7)
> install.packages("mctest")
> library(mctest)
> omcdiag(cps[,c(-6)], cps$wage) # or "omcdiag(cps[,c(1:5,7:11)], cps$wage)" will work as well.
Call:
omcdiag(x = cps[, c(-6)], y = cps$wage)
Overall Multicollinearity Diagnostics
MC Results detection
Determinant |X'X|: 0.0001 1
Farrar Chi-Square: 4833.5751 1
Red Indicator: 0.1983 0
Sum of Lambda Inverse: 10068.8439 1
Theil's Method: 1.2263 1
Condition Number: 739.7337 1
1 --> COLLINEARITY is detected by the test
0 --> COLLINEARITY is not detected by the test
>
> imcdiag(cps[,c(-6)],cps$wage)
Call:
imcdiag(x = cps[, c(-6)], y = cps$wage)
All Individual Multicollinearity Diagnostics Result
VIF TOL Wi Fi Leamer CVIF Klein
education 231.1956 0.0043 13402.4982 15106.5849 0.0658 236.4725 1
south 1.0468 0.9553 2.7264 3.0731 0.9774 1.0707 0
sex 1.0916 0.9161 5.3351 6.0135 0.9571 1.1165 0
experience 5184.0939 0.0002 301771.2445 340140.5368 0.0139 5302.4188 1
union 1.1209 0.8922 7.0368 7.9315 0.9445 1.1464 0
age 4645.6650 0.0002 270422.7164 304806.1391 0.0147 4751.7005 1
race 1.0371 0.9642 2.1622 2.4372 0.9819 1.0608 0
occupation 1.2982 0.7703 17.3637 19.5715 0.8777 1.3279 0
sector 1.1987 0.8343 11.5670 13.0378 0.9134 1.2260 0
marr 1.0961 0.9123 5.5969 6.3085 0.9551 1.1211 0
1 --> COLLINEARITY is detected by the test
0 --> COLLINEARITY is not detected by the test
education , south , experience , age , race , occupation , sector , marr , coefficient(s) are non-significant may be due to multicollinearity
R-square of y on all x: 0.2805
* use method argument to check which regressors may be the reason of collinearity
===================================
>
> round(pcor(cps[,c(-6)], method = "pearson")$estimate,4)
education south sex experience union age race occupation sector marr
education 1.0000 -0.0318 0.0515 -0.9976 -0.0075 0.9973 0.0172 0.0294 -0.0213 -0.0403
south -0.0318 1.0000 -0.0302 -0.0223 -0.0975 0.0215 -0.1112 0.0084 -0.0215 0.0304
sex 0.0515 -0.0302 1.0000 0.0550 -0.1201 -0.0537 0.0200 -0.1428 -0.1121 0.0042
experience -0.9976 -0.0223 0.0550 1.0000 -0.0102 0.9999 0.0109 0.0421 -0.0133 -0.0410
union -0.0075 -0.0975 -0.1201 -0.0102 1.0000 0.0122 -0.1077 0.2130 -0.0135 0.0689
age 0.9973 0.0215 -0.0537 0.9999 0.0122 1.0000 -0.0108 -0.0441 0.0146 0.0451
race 0.0172 -0.1112 0.0200 0.0109 -0.1077 -0.0108 1.0000 0.0575 0.0064 0.0556
occupation 0.0294 0.0084 -0.1428 0.0421 0.2130 -0.0441 0.0575 1.0000 0.3147 -0.0186
sector -0.0213 -0.0215 -0.1121 -0.0133 -0.0135 0.0146 0.0064 0.3147 1.0000 0.0365
marr -0.0403 0.0304 0.0042 -0.0410 0.0689 0.0451 0.0556 -0.0186 0.0365 1.0000
> lm2 = lm(log(cps$wage) ~ . -age , data = cps)
> summary(lm2)
Call:
lm(formula = log(cps$wage) ~ . - age, data = cps)
Residuals:
Min 1Q Median 3Q Max
-2.16044 -0.29073 -0.00505 0.29994 1.97997
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.562676 0.160116 3.514 0.000479 ***
education 0.094135 0.008188 11.497 < 2e-16 ***
south -0.103071 0.042796 -2.408 0.016367 *
sex -0.220344 0.039834 -5.532 5.02e-08 ***
experience 0.010335 0.001746 5.919 5.86e-09 ***
union 0.199987 0.052450 3.813 0.000154 ***
race 0.050643 0.028519 1.776 0.076345 .
occupation -0.006971 0.013091 -0.532 0.594619
sector 0.091022 0.038717 2.351 0.019094 *
marr 0.075152 0.041872 1.795 0.073263 .
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.4397 on 524 degrees of freedom
Multiple R-squared: 0.3177, Adjusted R-squared: 0.306
F-statistic: 27.11 on 9 and 524 DF, p-value: < 2.2e-16
> anova(lm1, lm2)
Analysis of Variance Table
Model 1: log(cps$wage) ~ education + south + sex + experience + union +
age + race + occupation + sector + marr
Model 2: log(cps$wage) ~ (education + south + sex + experience + union +
age + race + occupation + sector + marr) - age
Res.Df RSS Df Sum of Sq F Pr(>F)
1 523 101.17
2 524 101.28 -1 -0.11518 0.5954 0.4407
>
multicolinearity.1545758501.txt.gz · Last modified: by hkimscil