This is an old revision of the document!
Table of Contents
Gradient Descent
explanation
Why normalize (scale or make z-score) xi
x 변인의 측정단위로 인해서 b 값이 결정되게 되는데 이 때의 b값은 상당하고 다양한 범위를 가질 수 있다. 가령 월 수입이 (인컴) X 라고 한다면 우리가 추정해야 (추적해야) 할 b값은 수백만이 될 수도 있다.이 값을 gradient로 추적하게 된다면 너무도 많은 iteration을 거쳐야 할 수 있다. 변인이 바뀌면 이 b의 추적범위도 드라마틱하게 바뀌게 된다. 이를 표준화한 x 점수를 사용하게 된다면 일정한 learning rate와 iteration만으로도 정확한 a와 b를 추적할 수 있게 된다.
How to unnormalize (unscale) a and b
\begin{eqnarray*} y & = & a + b * x \\ & & \text{we use z instead of x} \\ & & \text{and } \\ & & z = \frac{(x - \mu)}{\sigma} \\ & & \text{suppose that the result after calculation be } \\ y & = & k + m * z \\ & = & k + m * \frac{(x - \mu)}{\sigma} \\ & = & k + \frac{m * x}{\sigma} - \frac{m * \mu}{\sigma} \\ & = & k - \frac{m * \mu}{\sigma} + \frac{m * x}{\sigma} \\ & = & k - \frac{\mu}{\sigma} * m + \frac{m}{\sigma} * x \\ & & \text{therefore, a and be that we try to get are } \\ a & = & k - \frac{\mu}{\sigma} * m \\ b & = & \frac{m}{\sigma} \\ \end{eqnarray*}
R code: Idea
library(ggplot2)
library(ggpmisc)
rm(list=ls())
# set.seed(191)
nx <- 200
mx <- 4.5
sdx <- mx * 0.56
x <- rnorm(nx, mx, sdx)
slp <- 12
y <- slp * x + rnorm(nx, 0, slp*sdx*3)
data <- data.frame(x, y)
mo <- lm(y ~ x, data = data)
summary(mo)
ggplot(data = data, aes(x = x, y = y)) +
geom_point() +
stat_poly_line() +
stat_poly_eq(use_label(c("eq", "R2"))) +
theme_classic()
# set.seed(191)
# Initialize random betas
# 우선 b를 고정하고 a만
# 변화시켜서 이해
b <- summary(mo)$coefficients[2]
a <- 0
b.init <- b
a.init <- a
# Predict function:
predict <- function(x, a, b){
return (a + b * x)
}
# And loss function is:
residuals <- function(predictions, y) {
return(y - predictions)
}
# we use sum of square of error which oftentimes become big
ssrloss <- function(predictions, y) {
residuals <- (y - predictions)
return(sum(residuals^2))
}
ssrs <- c() # for sum of square residuals
srs <- c() # sum of residuals
as <- c() # for as (intercepts)
for (i in seq(from = -50, to = 50, by = 0.01)) {
pred <- predict(x, i, b)
res <- residuals(pred, y)
ssr <- ssrloss(pred, y)
ssrs <- append(ssrs, ssr)
srs <- append(srs, sum(res))
as <- append(as, i)
}
length(ssrs)
length(srs)
length(as)
min(ssrs)
min.pos.ssrs <- which(ssrs == min(ssrs))
min.pos.ssrs
print(as[min.pos.ssrs])
summary(mo)
plot(seq(1, length(ssrs)), ssrs)
plot(seq(1, length(ssrs)), srs)
tail(ssrs)
max(ssrs)
min(ssrs)
tail(srs)
max(srs)
min(srs)
output
>
>
>
> library(ggplot2)
> library(ggpmisc)
>
> rm(list=ls())
> # set.seed(191)
> nx <- 200
> mx <- 4.5
> sdx <- mx * 0.56
> x <- rnorm(nx, mx, sdx)
> slp <- 12
> y <- slp * x + rnorm(nx, 0, slp*sdx*3)
>
> data <- data.frame(x, y)
>
> mo <- lm(y ~ x, data = data)
> summary(mo)
Call:
lm(formula = y ~ x, data = data)
Residuals:
Min 1Q Median 3Q Max
-259.314 -59.215 6.683 58.834 309.833
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 8.266 12.546 0.659 0.511
x 11.888 2.433 4.887 2.11e-06 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 88.57 on 198 degrees of freedom
Multiple R-squared: 0.1076, Adjusted R-squared: 0.1031
F-statistic: 23.88 on 1 and 198 DF, p-value: 2.111e-06
>
> ggplot(data = data, aes(x = x, y = y)) +
+ geom_point() +
+ stat_poly_line() +
+ stat_poly_eq(use_label(c("eq", "R2"))) +
+ theme_classic()
> # set.seed(191)
> # Initialize random betas
> # 우선 b를 고정하고 a만
> # 변화시켜서 이해
> b <- summary(mo)$coefficients[2]
> a <- 0
>
> b.init <- b
> a.init <- a
>
> # Predict function:
> predict <- function(x, a, b){
+ return (a + b * x)
+ }
>
> # And loss function is:
> residuals <- function(predictions, y) {
+ return(y - predictions)
+ }
>
> # we use sum of square of error which oftentimes become big
> ssrloss <- function(predictions, y) {
+ residuals <- (y - predictions)
+ return(sum(residuals^2))
+ }
>
> ssrs <- c() # for sum of square residuals
> srs <- c() # sum of residuals
> as <- c() # for as (intercepts)
>
> for (i in seq(from = -50, to = 50, by = 0.01)) {
+ pred <- predict(x, i, b)
+ res <- residuals(pred, y)
+ ssr <- ssrloss(pred, y)
+ ssrs <- append(ssrs, ssr)
+ srs <- append(srs, sum(res))
+ as <- append(as, i)
+ }
> length(ssrs)
[1] 10001
> length(srs)
[1] 10001
> length(as)
[1] 10001
>
> min(ssrs)
[1] 1553336
> min.pos.ssrs <- which(ssrs == min(ssrs))
> min.pos.ssrs
[1] 5828
> print(as[min.pos.ssrs])
[1] 8.27
> summary(mo)
Call:
lm(formula = y ~ x, data = data)
Residuals:
Min 1Q Median 3Q Max
-259.314 -59.215 6.683 58.834 309.833
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 8.266 12.546 0.659 0.511
x 11.888 2.433 4.887 2.11e-06 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 88.57 on 198 degrees of freedom
Multiple R-squared: 0.1076, Adjusted R-squared: 0.1031
F-statistic: 23.88 on 1 and 198 DF, p-value: 2.111e-06
> plot(seq(1, length(ssrs)), ssrs)
> plot(seq(1, length(ssrs)), srs)
> tail(ssrs)
[1] 1900842 1901008 1901175 1901342 1901509 1901676
> max(ssrs)
[1] 2232329
> min(ssrs)
[1] 1553336
> tail(srs)
[1] -8336.735 -8338.735 -8340.735 -8342.735 -8344.735 -8346.735
> max(srs)
[1] 11653.26
> min(srs)
[1] -8346.735
>
>
위 방법은 dumb . . . . .
우선 a의 범위가 어디가 될지 몰라서 -10 에서 10까지로 한것
이 두 지점 사이를 0.01 단위로 증가시킨 값을 a값이라고 할 때의 mse값을 구하여 저장한 것
이렇게 구한 mse 값들 중 최소값일 때의 a값을 regression의 a값으로 추정한 것.
이렇게 말고 구할 수 있는 방법은 없을까?
gradient descent
Gradient descend
위에서 a값이 무엇일 때 mse값이 최소가 될까를 봐서 이 때의 a값을 실제 $y = a + bx$ 의 a 값으로 삼았다. 이 때 a값의 추정을 위해서
seq(-10, 10, 0.01) 의 범위와 증가값을 가지고 일일이 대입하여 mse를 구아였다.
위에서의 0.01씩 증가시켜 대입하는 것이 아니라 처음 한 숫자에서 시작한 후 그 다음 숫자를 정한 후에 점진적으로 그 숫자 간격을 줄여가면서 보면 정율적으로 0.01씩 증가시키는 것 보다 효율적일 것 같다. 이 증가분을 구하기 위해서 미분을 사용한다.
점차하강 = 조금씩 깍아서 원하는 기울기 (미분값) 찾기
prerequisite:
표준편차 추론에서 평균을 사용하는 이유: 실험적_수학적_이해
deriviation of a and b in a simple regression
위의 문서는 a, b에 대한 값을 미분법을 이용해서 직접 구하였다. 컴퓨터로는 이렇게 하기가 쉽지 않다. 그렇다면 이 값을 반복계산을 이용해서 추출하는 방법은 없을까? gradient descent
\begin{eqnarray*}
\text{for a (constant)} \\
\\
\text{SSE} & = & \text{Sum of Square Residuals} \\
\text{Residual} & = & (Y_i - (a + bX_i)) \\
\\
\frac{\text{dSSE}}{\text{da}}
& = & \frac{\text{dResidual^2}}{\text{dResidual}} * \frac{\text{dResidual}}{\text{da}} \\
& = & 2 * \text{Residual} * \dfrac{\text{d}}{\text{da}} (Y_i - (a+bX_i)) \\
& \because & \dfrac{\text{d}}{\text{da}} (Y_i - (a+bX_i)) = -1 \\
& = & 2 * \sum{(Y_i - (a + bX_i))} * -1 \\
& = & -2 *\sum{\text{Residual}} \\
\end{eqnarray*}
아래 R code에서 gradient function을 참조.
\begin{eqnarray*} \text{for b, (coefficient)} \\ \\ \dfrac{\text{d}}{\text{db}} \sum{(Y_i - (a + bX_i))^2} & = & \sum{\dfrac{\text{dResidual}^2}{\text{db}}} \\ & = & \sum{\dfrac{\text{dResidual}^2}{\text{dResidual}}*\dfrac{\text{dResidual}}{\text{db}} } \\ & = & \sum{2*\text{Residual} * \dfrac{\text{dResidual}}{\text{db}} } \\ & = & \sum{2*\text{Residual} * (-X_i) } \;\;\;\; \\ & \because & \dfrac{\text{dResidual}}{\text{db}} = (Y_i - (a+bX_i)) = -X_i \\ & = & -2 X_i \sum{(Y_i - (a + bX_i))} \\ & = & -2 * X_i * \sum{\text{residual}} \\ \\ \end{eqnarray*}
(미분을 이해한다는 것을 전제로) 위의 식은 b값이 변할 때 msr (mean square residual) 값이 어떻게 변하는가를 알려주는 것이다. 그리고 그것은 b값에 대한 residual의 총합에 (-2/N)*X값을 곱한 값이다.
gradient <- function(x, y, predictions){
error = y - predictions
db = -2 * mean(x * error)
da = -2 * mean(error)
return(list("b" = db, "a" = da))
}
위 펑션으로 얻은 da와 db값을 초기에 설정한 a, b 값에 더해 준 값을 다시 a, b값으로 하여 gradient 펑션을 통해서 다시 db, da값을 구하고 이를 다시 이전 단계에서 구한 a, b값에 더하여 그 값을 다시 a, b값을 하여 . . . .
위를 반복한다. 단, db값과 da값을 그냥 대입하기 보다는 초기에 설정한 learning.rate값을 (0.01 예를 들면) 곱하여 구한 값을 더하게 된다. 이것이 아래의 code이다.
gradient <- function(x, y, predictions){
error = y - predictions
db = -2 * mean(x * error)
da = -2 * mean(error)
return(list("b" = db, "a" = da))
}
mseloss <- function(predictions, y) {
residuals <- (y - predictions)
return(mean(residuals^2))
}
# Train the model with scaled features
learning_rate = 1e-2
lr = 1e-1
# Record Loss for each epoch:
logs = list()
as = c()
bs = c()
mse = c()
sse = c()
x.ori <- x
zx <- (x-mean(x))/sd(x)
nlen <- 50
for (epoch in 1:nlen) {
predictions <- predict(zx, a, b)
loss <- mseloss(predictions, y)
mse <- append(mse, loss)
grad <- gradient(zx, y, predictions)
step.b <- grad$b * lr
step.a <- grad$a * lr
b <- b-step.b
a <- a-step.a
as <- append(as, a)
bs <- append(bs, b)
}
R code
# d statquest explanation
# x <- c(0.5, 2.3, 2.9)
# y <- c(1.4, 1.9, 3.2)
rm(list=ls())
# set.seed(191)
n <- 300
x <- rnorm(n, 5, 1.2)
y <- 2.14 * x + rnorm(n, 0, 4)
# data <- data.frame(x, y)
data <- tibble(x = x, y = y)
mo <- lm(y~x)
summary(mo)
# set.seed(191)
# Initialize random betas
b1 = rnorm(1)
b0 = rnorm(1)
b1.init <- b1
b0.init <- b0
# Predict function:
predict <- function(x, b0, b1){
return (b0 + b1 * x)
}
# And loss function is:
residuals <- function(predictions, y) {
return(y - predictions)
}
loss_mse <- function(predictions, y){
residuals = y - predictions
return(mean(residuals ^ 2))
}
predictions <- predict(x, b0, b1)
residuals <- residuals(predictions, y)
loss = loss_mse(predictions, y)
data <- tibble(data.frame(x, y, predictions, residuals))
print(paste0("Loss is: ", round(loss)))
gradient <- function(x, y, predictions){
dinputs = y - predictions
db1 = -2 * mean(x * dinputs)
db0 = -2 * mean(dinputs)
return(list("db1" = db1, "db0" = db0))
}
gradients <- gradient(x, y, predictions)
print(gradients)
# Train the model with scaled features
x_scaled <- (x - mean(x)) / sd(x)
learning_rate = 1e-1
# Record Loss for each epoch:
# logs = list()
# bs=list()
b0s = c()
b1s = c()
mse = c()
nlen <- 80
for (epoch in 1:nlen){
# Predict all y values:
predictions = predict(x_scaled, b0, b1)
loss = loss_mse(predictions, y)
mse = append(mse, loss)
# logs = append(logs, loss)
if (epoch %% 10 == 0){
print(paste0("Epoch: ",epoch, ", Loss: ", round(loss, 5)))
}
gradients <- gradient(x_scaled, y, predictions)
db1 <- gradients$db1
db0 <- gradients$db0
b1 <- b1 - db1 * learning_rate
b0 <- b0 - db0 * learning_rate
b0s <- append(b0s, b0)
b1s <- append(b1s, b1)
}
# unscale coefficients to make them comprehensible
b0 = b0 - (mean(x) / sd(x)) * b1
b1 = b1 / sd(x)
# changes of estimators
b0s <- b0s - (mean(x) /sd(x)) * b1s
b1s <- b1s / sd(x)
parameters <- tibble(data.frame(b0s, b1s, mse))
cat(paste0("Slope: ", b1, ", \n", "Intercept: ", b0, "\n"))
summary(lm(y~x))$coefficients
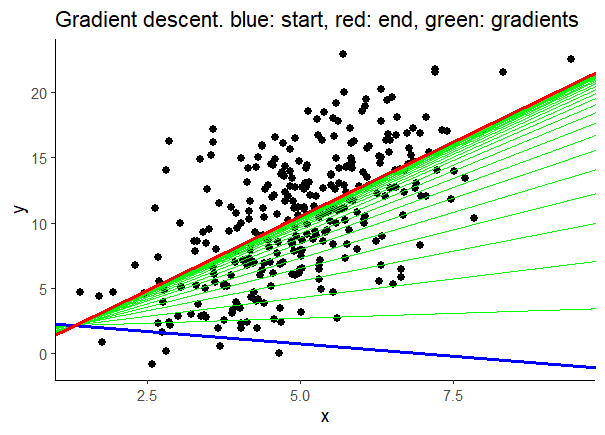
ggplot(data, aes(x = x, y = y)) +
geom_point(size = 2) +
geom_abline(aes(intercept = b0s, slope = b1s),
data = parameters, linewidth = 0.5,
color = 'green') +
theme_classic() +
geom_abline(aes(intercept = b0s, slope = b1s),
data = parameters %>% slice_head(),
linewidth = 1, color = 'blue') +
geom_abline(aes(intercept = b0s, slope = b1s),
data = parameters %>% slice_tail(),
linewidth = 1, color = 'red') +
labs(title = 'Gradient descent. blue: start, red: end, green: gradients')
b0.init
b1.init
data
parameters
R output
> rm(list=ls())
> # set.seed(191)
> n <- 300
> x <- rnorm(n, 5, 1.2)
> y <- 2.14 * x + rnorm(n, 0, 4)
>
> # data <- data.frame(x, y)
> data <- tibble(x = x, y = y)
>
> mo <- lm(y~x)
> summary(mo)
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-9.754 -2.729 -0.135 2.415 10.750
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.7794 0.9258 -0.842 0.401
x 2.2692 0.1793 12.658 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 3.951 on 298 degrees of freedom
Multiple R-squared: 0.3497, Adjusted R-squared: 0.3475
F-statistic: 160.2 on 1 and 298 DF, p-value: < 2.2e-16
>
> # set.seed(191)
> # Initialize random betas
> b1 = rnorm(1)
> b0 = rnorm(1)
>
> b1.init <- b1
> b0.init <- b0
>
> # Predict function:
> predict <- function(x, b0, b1){
+ return (b0 + b1 * x)
+ }
>
> # And loss function is:
> residuals <- function(predictions, y) {
+ return(y - predictions)
+ }
>
> loss_mse <- function(predictions, y){
+ residuals = y - predictions
+ return(mean(residuals ^ 2))
+ }
>
> predictions <- predict(x, b0, b1)
> residuals <- residuals(predictions, y)
> loss = loss_mse(predictions, y)
>
> data <- tibble(data.frame(x, y, predictions, residuals))
>
> print(paste0("Loss is: ", round(loss)))
[1] "Loss is: 393"
>
> gradient <- function(x, y, predictions){
+ dinputs = y - predictions
+ db1 = -2 * mean(x * dinputs)
+ db0 = -2 * mean(dinputs)
+
+ return(list("db1" = db1, "db0" = db0))
+ }
>
> gradients <- gradient(x, y, predictions)
> print(gradients)
$db1
[1] -200.6834
$db0
[1] -37.76994
>
> # Train the model with scaled features
> x_scaled <- (x - mean(x)) / sd(x)
>
> learning_rate = 1e-1
>
> # Record Loss for each epoch:
> # logs = list()
> # bs=list()
> b0s = c()
> b1s = c()
> mse = c()
>
> nlen <- 80
> for (epoch in 1:nlen){
+ # Predict all y values:
+ predictions = predict(x_scaled, b0, b1)
+ loss = loss_mse(predictions, y)
+ mse = append(mse, loss)
+ # logs = append(logs, loss)
+
+ if (epoch %% 10 == 0){
+ print(paste0("Epoch: ",epoch, ", Loss: ", round(loss, 5)))
+ }
+
+ gradients <- gradient(x_scaled, y, predictions)
+ db1 <- gradients$db1
+ db0 <- gradients$db0
+
+ b1 <- b1 - db1 * learning_rate
+ b0 <- b0 - db0 * learning_rate
+ b0s <- append(b0s, b0)
+ b1s <- append(b1s, b1)
+ }
[1] "Epoch: 10, Loss: 18.5393"
[1] "Epoch: 20, Loss: 15.54339"
[1] "Epoch: 30, Loss: 15.50879"
[1] "Epoch: 40, Loss: 15.50839"
[1] "Epoch: 50, Loss: 15.50839"
[1] "Epoch: 60, Loss: 15.50839"
[1] "Epoch: 70, Loss: 15.50839"
[1] "Epoch: 80, Loss: 15.50839"
>
> # unscale coefficients to make them comprehensible
> b0 = b0 - (mean(x) / sd(x)) * b1
> b1 = b1 / sd(x)
>
> # changes of estimators
> b0s <- b0s - (mean(x) /sd(x)) * b1s
> b1s <- b1s / sd(x)
>
> parameters <- tibble(data.frame(b0s, b1s, mse))
>
> cat(paste0("Slope: ", b1, ", \n", "Intercept: ", b0, "\n"))
Slope: 2.26922511738252,
Intercept: -0.779435058320381
> summary(lm(y~x))$coefficients
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.7794352 0.9258064 -0.8418986 4.005198e-01
x 2.2692252 0.1792660 12.6584242 1.111614e-29
>
> ggplot(data, aes(x = x, y = y)) +
+ geom_point(size = 2) +
+ geom_abline(aes(intercept = b0s, slope = b1s),
+ data = parameters, linewidth = 0.5,
+ color = 'green') +
+ theme_classic() +
+ geom_abline(aes(intercept = b0s, slope = b1s),
+ data = parameters %>% slice_head(),
+ linewidth = 1, color = 'blue') +
+ geom_abline(aes(intercept = b0s, slope = b1s),
+ data = parameters %>% slice_tail(),
+ linewidth = 1, color = 'red') +
+ labs(title = 'Gradient descent. blue: start, red: end, green: gradients')
>
> b0.init
[1] -1.67967
> b1.init
[1] -1.323992
>
> data
# A tibble: 300 × 4
x y predictions residuals
<dbl> <dbl> <dbl> <dbl>
1 4.13 6.74 -7.14 13.9
2 7.25 14.0 -11.3 25.3
3 6.09 13.5 -9.74 23.3
4 6.29 15.1 -10.0 25.1
5 4.40 3.81 -7.51 11.3
6 6.03 13.9 -9.67 23.5
7 6.97 12.1 -10.9 23.0
8 4.84 12.8 -8.09 20.9
9 6.85 17.2 -10.7 28.0
10 3.33 3.80 -6.08 9.88
# ℹ 290 more rows
# ℹ Use `print(n = ...)` to see more rows
> parameters
# A tibble: 80 × 3
b0s b1s mse
<dbl> <dbl> <dbl>
1 2.67 -0.379 183.
2 1.99 0.149 123.
3 1.44 0.571 84.3
4 1.00 0.910 59.6
5 0.652 1.18 43.7
6 0.369 1.40 33.6
7 0.142 1.57 27.1
8 -0.0397 1.71 22.9
9 -0.186 1.82 20.2
10 -0.303 1.91 18.5
# ℹ 70 more rows
#