This is an old revision of the document!
Gradient Descent
점차하강 = 조금씩 깍아서 원하는 기울기 (미분값) 찾기
prerequisite:
표준편차 추론에서 평균을 사용하는 이유: 실험적_수학적_이해
deriviation of a and b in a simple regression
위의 문서는 a, b에 대한 값을 미분법을 이용해서 직접 구하였다. 컴퓨터로는 이렇게 하기가 쉽지 않다. 그렇다면 이 값을 반복계산을 이용해서 추출하는 방법은 없을까? gradient descent
우선 위의 문서에서 (두번째) 최소값이 되는 SS값을 찾는다고 설명했는데, 이는 MS값으로 대체해서 생각해도 된다.
\begin{eqnarray*} \text{MS} & = & \frac {\text{SS}}{n} \end{eqnarray*}
\begin{eqnarray*} \text{for a (constant)} \\ \\ \dfrac{\text{d}}{\text{dv}} \text{MSE (Mean Square Error)} & = & \dfrac{\text{d}}{\text{dv}} \frac {\sum{(Y_i - (a + bX_i))^2}} {N} \\ & = & \sum \dfrac{\text{d}}{\text{dv}} \frac{{(Y_i - (a + bX_i))^2}} {N} \\ & = & \sum{2 \frac{1}{N} (Y_i - (a + bX_i))} * (-1) \;\;\;\; \\ & \because & \dfrac{\text{d}}{\text{dv for a}} (Y_i - (a+bX_i)) = -1 \\ & = & -2 \frac{1}{N} \sum{(Y_i - (a + bX_i))} \\ \end{eqnarray*}
library(tidyverse)
# a simple example
# statquest explanation
x <- c(0.5, 2.3, 2.9)
y <- c(1.4, 1.9, 3.2)
rm(list=ls())
# set.seed(191)
n <- 500
x <- rnorm(n, 5, 1.2)
y <- 2.14 * x + rnorm(n, 0, 4)
# data <- data.frame(x, y)
data <- tibble(x = x, y = y)
data
mo <- lm(y~x)
summary(mo)
# set.seed(191)
# Initialize random betas
b1 = rnorm(1)
b0 = rnorm(1)
# Predict function:
predict <- function(x, b0, b1){
return (b0 + b1 * x)
}
# And loss function is:
residuals <- function(predictions, y) {
return(y - predictions)
}
loss_mse <- function(predictions, y){
residuals = y - predictions
return(mean(residuals ^ 2))
}
predictions <- predict(x, b0, b1)
residuals <- residuals(predictions, y)
loss = loss_mse(predictions, y)
temp.sum <- data.frame(x, y, b0, b1,predictions, residuals)
temp.sum
print(paste0("Loss is: ", round(loss)))
gradient <- function(x, y, predictions){
dinputs = y - predictions
db1 = -2 * mean(x * dinputs)
db0 = -2 * mean(dinputs)
return(list("db1" = db1, "db0" = db0))
}
gradients <- gradient(x, y, predictions)
print(gradients)
# Train the model with scaled features
x_scaled <- (x - mean(x)) / sd(x)
learning_rate = 1e-1
# Record Loss for each epoch:
logs = list()
bs=list()
b0s = c()
b1s = c()
msr = c()
nlen <- 80
for (epoch in 1:nlen){
# Predict all y values:
predictions = predict(x_scaled, b0, b1)
loss = loss_mse(predictions, y)
msr = append(msr, loss)
logs = append(logs, loss)
if (epoch %% 10 == 0){
print(paste0("Epoch: ",epoch, ", Loss: ", round(loss, 5)))
}
gradients <- gradient(x_scaled, y, predictions)
db1 <- gradients$db1
db0 <- gradients$db0
b1 <- b1 - db1 * learning_rate
b0 <- b0 - db0 * learning_rate
b0s <- append(b0s, b0)
b1s <- append(b1s, b1)
}
# I must unscale coefficients to make them comprehensible
b0 = b0 - (mean(x) / sd(x)) * b1
b1 = b1 / sd(x)
b0s <- b0s - (mean(x) /sd(x)) * b1s
b1s <- b1s / sd(x)
parameters <- tibble(data.frame(b0s, b1s, msr))
cat(paste0("Inclination: ", b1, ", \n", "Intercept: ", b0, "\n"))
summary(lm(y~x))$coefficients
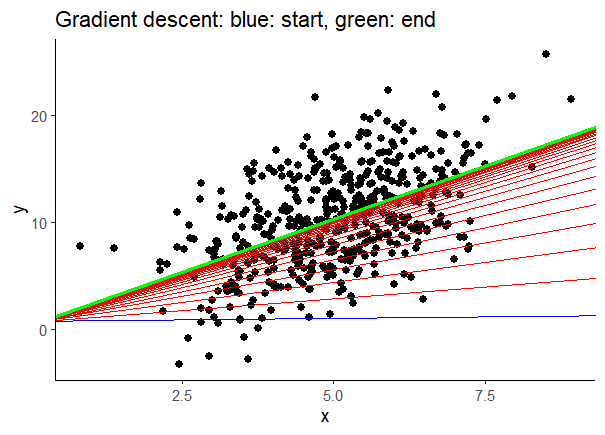
ggplot(data, aes(x = x, y = y)) +
geom_point(size = 2) +
geom_abline(aes(intercept = b0s, slope = b1s),
data = parameters, linewidth = 0.5, color = 'red') +
theme_classic() +
geom_abline(aes(intercept = b0s, slope = b1s),
data = parameters %>% slice_head(),
linewidth = 0.5, color = 'blue') +
geom_abline(aes(intercept = b0s, slope = b1s),
data = parameters %>% slice_tail(),
linewidth = 1, color = 'green') +
labs(title = 'Gradient descent: blue: start, green: end')
data
parameters
> # d statquest explanation
> x <- c(0.5, 2.3, 2.9)
> y <- c(1.4, 1.9, 3.2)
>
> rm(list=ls())
> # set.seed(191)
> n <- 500
> x <- rnorm(n, 5, 1.2)
> y <- 2.14 * x + rnorm(n, 0, 4)
>
> # data <- data.frame(x, y)
> data <- tibble(x = x, y = y)
> data
# A tibble: 500 × 2
x y
<dbl> <dbl>
1 6.78 10.6
2 7.17 17.2
3 4.63 5.80
4 3.12 10.5
5 5.65 9.68
6 5.12 10.8
7 4.05 16.8
8 7.27 16.5
9 4.13 3.96
10 5.27 13.9
# ℹ 490 more rows
# ℹ Use `print(n = ...)` to see more rows
>
> mo <- lm(y~x)
> summary(mo)
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-10.474 -2.999 0.095 2.591 11.868
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.4613 0.7339 0.629 0.53
x 1.9828 0.1427 13.890 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 3.929 on 498 degrees of freedom
Multiple R-squared: 0.2792, Adjusted R-squared: 0.2778
F-statistic: 192.9 on 1 and 498 DF, p-value: < 2.2e-16
>
> # set.seed(191)
> # Initialize random betas
> b1 = rnorm(1)
> b0 = rnorm(1)
>
> # Predict function:
> predict <- function(x, b0, b1){
+ return (b0 + b1 * x)
+ }
>
> # And loss function is:
> residuals <- function(predictions, y) {
+ return(y - predictions)
+ }
>
> loss_mse <- function(predictions, y){
+ residuals = y - predictions
+ return(mean(residuals ^ 2))
+ }
>
> predictions <- predict(x, b0, b1)
> residuals <- residuals(predictions, y)
> loss = loss_mse(predictions, y)
>
> temp.sum <- data.frame(x, y, b0, b1,predictions, residuals)
> temp.sum
x y b0 b1 predictions residuals
1 6.7787032 10.5653561 -1.264277 -0.5262407 -4.831506 15.3968625
2 7.1666745 17.2133136 -1.264277 -0.5262407 -5.035673 22.2489863
3 4.6255226 5.7995419 -1.264277 -0.5262407 -3.698415 9.4979572
4 3.1188584 10.4865173 -1.264277 -0.5262407 -2.905547 13.3920646
5 5.6541258 9.6787933 -1.264277 -0.5262407 -4.239708 13.9185013
6 5.1232990 10.8138626 -1.264277 -0.5262407 -3.960365 14.7742280
7 4.0510211 16.7630100 -1.264277 -0.5262407 -3.396089 20.1590992
8 7.2687149 16.4785689 -1.264277 -0.5262407 -5.089370 21.5679393
9 4.1333064 3.9624439 -1.264277 -0.5262407 -3.439391 7.4018350
10 5.2672548 13.9111428 -1.264277 -0.5262407 -4.036121 17.9472636
11 5.5156223 11.2320867 -1.264277 -0.5262407 -4.166822 15.3989085
12 3.1799040 6.1446257 -1.264277 -0.5262407 -2.937672 9.0822976
13 6.7547841 10.0729772 -1.264277 -0.5262407 -4.818919 14.8918964
14 7.2250923 7.4743490 -1.264277 -0.5262407 -5.066414 12.5407635
15 5.6642827 6.1278221 -1.264277 -0.5262407 -4.245053 10.3728751
16 6.4099293 16.6274813 -1.264277 -0.5262407 -4.637443 21.2649238
17 4.2914899 11.2173980 -1.264277 -0.5262407 -3.522634 14.7400316
18 4.6413358 8.0794876 -1.264277 -0.5262407 -3.706737 11.7862243
19 5.6684969 7.1059092 -1.264277 -0.5262407 -4.247271 11.3531799
20 5.3803989 10.4308559 -1.264277 -0.5262407 -4.095662 14.5265177
21 4.0240137 4.0767913 -1.264277 -0.5262407 -3.381877 7.4586681
22 5.0816903 9.5443887 -1.264277 -0.5262407 -3.938469 13.4828579
23 6.4856995 2.8470186 -1.264277 -0.5262407 -4.677316 7.5243345
24 4.1315971 15.0691180 -1.264277 -0.5262407 -3.438492 18.5076095
25 4.3975735 10.0977703 -1.264277 -0.5262407 -3.578459 13.6762295
26 3.6800792 14.8057519 -1.264277 -0.5262407 -3.200884 18.0066364
27 5.9063058 14.7436966 -1.264277 -0.5262407 -4.372415 19.1161120
28 4.0259638 5.7319405 -1.264277 -0.5262407 -3.382903 9.1148435
29 5.6966522 9.5224078 -1.264277 -0.5262407 -4.262087 13.7844950
30 3.8406098 10.1716630 -1.264277 -0.5262407 -3.285362 13.4570252
31 3.7738837 10.1961941 -1.264277 -0.5262407 -3.250248 13.4464424
32 4.8977716 14.6487758 -1.264277 -0.5262407 -3.841684 18.4904595
33 3.5182859 -0.6639891 -1.264277 -0.5262407 -3.115742 2.4517532
34 6.7555953 18.3109425 -1.264277 -0.5262407 -4.819346 23.1302886
35 5.3450800 7.5049835 -1.264277 -0.5262407 -4.077076 11.5820590
36 4.6063392 3.7802993 -1.264277 -0.5262407 -3.688320 7.4686194
37 3.3150851 10.6463845 -1.264277 -0.5262407 -3.008810 13.6551942
38 2.1438875 5.5805865 -1.264277 -0.5262407 -2.392478 7.9730644
39 6.7867082 14.4541469 -1.264277 -0.5262407 -4.835719 19.2898659
40 7.1651170 16.0295592 -1.264277 -0.5262407 -5.034853 21.0644123
41 6.0068801 4.2186189 -1.264277 -0.5262407 -4.425342 8.6439606
42 3.8429583 6.8926969 -1.264277 -0.5262407 -3.286598 10.1792950
43 6.6963199 14.9606533 -1.264277 -0.5262407 -4.788153 19.7488062
44 5.9766522 17.5076500 -1.264277 -0.5262407 -4.409435 21.9170845
45 3.4139235 3.5029295 -1.264277 -0.5262407 -3.060823 6.5637521
46 7.1468347 15.4958432 -1.264277 -0.5262407 -5.025232 20.5210754
47 2.9413548 1.8553437 -1.264277 -0.5262407 -2.812138 4.6674813
48 2.7033044 4.8611663 -1.264277 -0.5262407 -2.686866 7.5480321
49 5.6384145 15.7331403 -1.264277 -0.5262407 -4.231440 19.9645804
50 3.6549025 13.8667532 -1.264277 -0.5262407 -3.187635 17.0543887
51 2.4549093 -3.2303197 -1.264277 -0.5262407 -2.556150 -0.6741695
52 3.4177686 5.1092427 -1.264277 -0.5262407 -3.062846 8.1720886
53 8.5165648 25.6896235 -1.264277 -0.5262407 -5.746040 31.4356634
54 5.6089046 8.3783769 -1.264277 -0.5262407 -4.215911 12.5942877
55 3.3871150 8.5696011 -1.264277 -0.5262407 -3.046715 11.6163159
56 4.4518647 6.5901035 -1.264277 -0.5262407 -3.607029 10.1971329
57 5.5052891 7.0080255 -1.264277 -0.5262407 -4.161384 11.1694096
58 4.6203097 9.7294702 -1.264277 -0.5262407 -3.695672 13.4251422
59 5.4313621 11.1323523 -1.264277 -0.5262407 -4.122481 15.2548330
60 4.6889464 15.0880915 -1.264277 -0.5262407 -3.731791 18.8198829
61 6.0363099 9.4591404 -1.264277 -0.5262407 -4.440829 13.8999693
62 5.9834349 15.5984185 -1.264277 -0.5262407 -4.413004 20.0114224
63 6.1256065 8.8309730 -1.264277 -0.5262407 -4.487820 13.3187934
64 4.7770683 8.5916899 -1.264277 -0.5262407 -3.778165 12.3698547
65 3.0977662 6.5005729 -1.264277 -0.5262407 -2.894448 9.3950206
66 7.2582566 10.1658760 -1.264277 -0.5262407 -5.083867 15.2497428
67 4.4274063 10.5254164 -1.264277 -0.5262407 -3.594158 14.1195747
68 4.4224093 15.3288304 -1.264277 -0.5262407 -3.591529 18.9203591
69 7.9562345 15.8094793 -1.264277 -0.5262407 -5.451171 21.2606505
70 6.1605765 17.6226869 -1.264277 -0.5262407 -4.506223 22.1289099
71 4.8811933 11.4006073 -1.264277 -0.5262407 -3.832960 15.2335669
72 5.8458839 8.8660352 -1.264277 -0.5262407 -4.340619 13.2066542
73 5.4176401 17.9873603 -1.264277 -0.5262407 -4.115260 22.1026199
74 5.1877292 10.0773562 -1.264277 -0.5262407 -3.994271 14.0716274
75 4.4385788 8.1866806 -1.264277 -0.5262407 -3.600038 11.7867184
76 6.5079686 16.8845586 -1.264277 -0.5262407 -4.689035 21.5735935
77 5.8326041 12.8972544 -1.264277 -0.5262407 -4.333631 17.2308850
78 4.7833622 10.1946848 -1.264277 -0.5262407 -3.781477 13.9761616
79 5.9256779 16.6025871 -1.264277 -0.5262407 -4.382610 20.9851969
80 4.9860307 12.9422586 -1.264277 -0.5262407 -3.888129 16.8303879
81 5.2401527 17.2049456 -1.264277 -0.5262407 -4.021859 21.2268042
82 6.7570239 13.8736266 -1.264277 -0.5262407 -4.820098 18.6937244
83 5.4384563 14.1770698 -1.264277 -0.5262407 -4.126214 18.3032838
84 5.4498287 12.0591785 -1.264277 -0.5262407 -4.132199 16.1913771
85 5.9643832 13.8220440 -1.264277 -0.5262407 -4.402978 18.2250221
86 4.4057387 8.0541411 -1.264277 -0.5262407 -3.582756 11.6368971
87 3.6834860 15.4963951 -1.264277 -0.5262407 -3.202677 18.6990723
88 6.4421163 9.7619937 -1.264277 -0.5262407 -4.654381 14.4163744
89 6.5442359 13.3216053 -1.264277 -0.5262407 -4.708120 18.0297254
90 5.9329826 8.1974096 -1.264277 -0.5262407 -4.386454 12.5838635
91 6.3086002 9.3337688 -1.264277 -0.5262407 -4.584119 13.9178879
92 6.6894199 9.9187932 -1.264277 -0.5262407 -4.784522 14.7033151
93 4.3681693 6.9327113 -1.264277 -0.5262407 -3.562985 10.4956967
94 6.6461515 12.5441888 -1.264277 -0.5262407 -4.761752 17.3059411
95 5.1824709 7.4015164 -1.264277 -0.5262407 -3.991504 11.3930204
96 2.1875381 1.6910838 -1.264277 -0.5262407 -2.415449 4.1065324
97 5.6086270 10.8605436 -1.264277 -0.5262407 -4.215765 15.0763083
98 5.4158031 7.6891953 -1.264277 -0.5262407 -4.114293 11.8034883
99 0.8135196 7.8181045 -1.264277 -0.5262407 -1.692384 9.5104888
100 3.7676048 9.5822003 -1.264277 -0.5262407 -3.246944 12.8291443
101 3.7048040 5.3532350 -1.264277 -0.5262407 -3.213896 8.5671307
102 4.5848668 8.3965243 -1.264277 -0.5262407 -3.677020 12.0735447
103 4.6436020 5.5043385 -1.264277 -0.5262407 -3.707929 9.2122678
104 5.5137839 19.8317442 -1.264277 -0.5262407 -4.165854 23.9975986
105 5.5460450 11.7004649 -1.264277 -0.5262407 -4.182832 15.8832965
106 2.6322855 8.5278252 -1.264277 -0.5262407 -2.649493 11.1773180
107 4.8768933 9.2744021 -1.264277 -0.5262407 -3.830697 13.1050988
108 4.2582660 15.6448394 -1.264277 -0.5262407 -3.505150 19.1499892
109 5.3263384 11.2636384 -1.264277 -0.5262407 -4.067213 15.3308513
110 4.7875378 7.8894584 -1.264277 -0.5262407 -3.783674 11.6731326
111 3.6879691 6.7596765 -1.264277 -0.5262407 -3.205036 9.9647129
112 4.2645818 9.7032671 -1.264277 -0.5262407 -3.508474 13.2117406
113 5.7080723 11.4807855 -1.264277 -0.5262407 -4.268097 15.7488824
114 4.4170445 11.9510702 -1.264277 -0.5262407 -3.588706 15.5397757
115 4.7051114 15.0610402 -1.264277 -0.5262407 -3.740298 18.8013383
116 3.2868115 2.0588466 -1.264277 -0.5262407 -2.993931 5.0527776
117 4.9496883 11.1438762 -1.264277 -0.5262407 -3.869004 15.0128806
118 5.3579592 10.4867567 -1.264277 -0.5262407 -4.083853 14.5706099
119 3.4340821 4.9124528 -1.264277 -0.5262407 -3.071431 7.9838836
120 7.5112322 15.4265323 -1.264277 -0.5262407 -5.216993 20.6435252
121 7.4090157 17.2211544 -1.264277 -0.5262407 -5.163202 22.3843568
122 5.3807003 12.0371465 -1.264277 -0.5262407 -4.095820 16.1329670
123 5.9982219 12.2743501 -1.264277 -0.5262407 -4.420785 16.6951354
124 3.0991733 0.5928870 -1.264277 -0.5262407 -2.895188 3.4880752
125 4.9540596 12.7552638 -1.264277 -0.5262407 -3.871305 16.6265686
126 5.4521347 13.9911543 -1.264277 -0.5262407 -4.133412 18.1245665
127 4.2101665 11.0247402 -1.264277 -0.5262407 -3.479838 14.5045782
128 2.1382146 6.3007539 -1.264277 -0.5262407 -2.389493 8.6902465
129 4.7861186 8.4328932 -1.264277 -0.5262407 -3.782927 12.2158206
130 4.6243029 12.1062901 -1.264277 -0.5262407 -3.697773 15.8040635
131 4.7045999 21.6574011 -1.264277 -0.5262407 -3.740029 25.3974300
132 5.0353365 9.1128945 -1.264277 -0.5262407 -3.914076 13.0269705
133 5.7684327 14.9482380 -1.264277 -0.5262407 -4.299861 19.2480990
134 5.4650414 11.1578444 -1.264277 -0.5262407 -4.140204 15.2980486
135 6.3983266 12.7511754 -1.264277 -0.5262407 -4.631337 17.3825121
136 5.1054629 12.2676585 -1.264277 -0.5262407 -3.950979 16.2186379
137 5.4727620 15.7361092 -1.264277 -0.5262407 -4.144267 19.8803762
138 4.7336163 10.1946145 -1.264277 -0.5262407 -3.755299 13.9499130
139 5.2480093 6.9764202 -1.264277 -0.5262407 -4.025993 11.0024132
140 3.0004377 2.7520590 -1.264277 -0.5262407 -2.843229 5.5952884
141 3.6651683 7.2627301 -1.264277 -0.5262407 -3.193038 10.4557678
142 4.5906320 3.7751924 -1.264277 -0.5262407 -3.680054 7.4552467
143 5.8844053 19.4617765 -1.264277 -0.5262407 -4.360890 23.8226670
144 3.5734761 14.9494035 -1.264277 -0.5262407 -3.144786 18.0941891
145 4.1928815 11.5554015 -1.264277 -0.5262407 -3.470742 15.0261434
146 6.8910946 12.6820411 -1.264277 -0.5262407 -4.890651 17.5726924
147 5.7008138 7.6449870 -1.264277 -0.5262407 -4.264277 11.9092641
148 3.6069183 14.5345051 -1.264277 -0.5262407 -3.162384 17.6968893
149 5.4279511 12.5578155 -1.264277 -0.5262407 -4.120686 16.6785012
150 5.6139766 11.8074150 -1.264277 -0.5262407 -4.218580 16.0259949
151 5.6023394 11.5063542 -1.264277 -0.5262407 -4.212456 15.7188101
152 6.2157176 8.5306942 -1.264277 -0.5262407 -4.535240 13.0659347
153 5.6589077 8.3478592 -1.264277 -0.5262407 -4.242224 12.5900837
154 2.8113763 1.9872925 -1.264277 -0.5262407 -2.743738 4.7310302
155 4.5806760 4.8901946 -1.264277 -0.5262407 -3.674815 8.5650098
156 5.6392284 13.7001285 -1.264277 -0.5262407 -4.231868 17.9319969
157 5.2827326 14.4966648 -1.264277 -0.5262407 -4.044266 18.5409307
158 4.4994363 4.2327446 -1.264277 -0.5262407 -3.632063 7.8648081
159 5.2554305 7.3630872 -1.264277 -0.5262407 -4.029898 11.3929856
160 5.5622164 9.0163544 -1.264277 -0.5262407 -4.191342 13.2076960
161 7.0995953 12.5898387 -1.264277 -0.5262407 -5.000373 17.5902115
162 5.6046834 12.2369786 -1.264277 -0.5262407 -4.213689 16.4506680
163 3.9260205 5.3385293 -1.264277 -0.5262407 -3.330309 8.6688381
164 6.6192734 16.2775842 -1.264277 -0.5262407 -4.747608 21.0251922
165 5.2875993 8.5628853 -1.264277 -0.5262407 -4.046827 12.6097122
166 4.3956646 8.8889738 -1.264277 -0.5262407 -3.577455 12.4664284
[ reached 'max' / getOption("max.print") -- omitted 334 rows ]
>
> print(paste0("Loss is: ", round(loss)))
[1] "Loss is: 228"
>
> gradient <- function(x, y, predictions){
+ dinputs = y - predictions
+ db1 = -2 * mean(x * dinputs)
+ db0 = -2 * mean(dinputs)
+
+ return(list("db1" = db1, "db0" = db0))
+ }
>
> gradients <- gradient(x, y, predictions)
> print(gradients)
$db1
[1] -149.8879
$db0
[1] -28.50182
>
> # Train the model with scaled features
> x_scaled <- (x - mean(x)) / sd(x)
>
> learning_rate = 1e-1
>
> # Record Loss for each epoch:
> logs = list()
> bs=list()
> b0s = c()
> b1s = c()
> msr = c()
>
> nlen <- 80
> for (epoch in 1:nlen){
+ # Predict all y values:
+ predictions = predict(x_scaled, b0, b1)
+ loss = loss_mse(predictions, y)
+ msr = append(msr, loss)
+
+ logs = append(logs, loss)
+
+ if (epoch %% 10 == 0){
+ print(paste0("Epoch: ",epoch, ", Loss: ", round(loss, 5)))
+ }
+
+ gradients <- gradient(x_scaled, y, predictions)
+ db1 <- gradients$db1
+ db0 <- gradients$db0
+
+ b1 <- b1 - db1 * learning_rate
+ b0 <- b0 - db0 * learning_rate
+ b0s <- append(b0s, b0)
+ b1s <- append(b1s, b1)
+ }
[1] "Epoch: 10, Loss: 17.96644"
[1] "Epoch: 20, Loss: 15.40245"
[1] "Epoch: 30, Loss: 15.37287"
[1] "Epoch: 40, Loss: 15.37253"
[1] "Epoch: 50, Loss: 15.37253"
[1] "Epoch: 60, Loss: 15.37253"
[1] "Epoch: 70, Loss: 15.37253"
[1] "Epoch: 80, Loss: 15.37253"
> # I must unscale coefficients to make them comprehensible
> b0 = b0 - (mean(x) / sd(x)) * b1
> b1 = b1 / sd(x)
>
> b0s <- b0s - (mean(x) /sd(x)) * b1s
> b1s <- b1s / sd(x)
>
> parameters <- tibble(data.frame(b0s, b1s, msr))
>
> cat(paste0("Inclination: ", b1, ", \n", "Intercept: ", b0, "\n"))
Inclination: 1.98275951151325,
Intercept: 0.461293071825862
> summary(lm(y~x))$coefficients
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.4612931 0.7339392 0.6285167 5.299537e-01
x 1.9827596 0.1427436 13.8903548 2.612507e-37
>
> ggplot(data, aes(x = x, y = y)) +
+ geom_point(size = 2) +
+ geom_abline(aes(intercept = b0s, slope = b1s),
+ data = parameters, linewidth = 0.5, color = 'red') +
+ theme_classic() +
+ geom_abline(aes(intercept = b0s, slope = b1s),
+ data = parameters %>% slice_head(),
+ linewidth = 0.5, color = 'blue') +
+ geom_abline(aes(intercept = b0s, slope = b1s),
+ data = parameters %>% slice_tail(),
+ linewidth = 1, color = 'green') +
+ labs(title = 'Gradient descent: blue: start, green: end')
> data
# A tibble: 500 × 2
x y
<dbl> <dbl>
1 6.78 10.6
2 7.17 17.2
3 4.63 5.80
4 3.12 10.5
5 5.65 9.68
6 5.12 10.8
7 4.05 16.8
8 7.27 16.5
9 4.13 3.96
10 5.27 13.9
# ℹ 490 more rows
# ℹ Use `print(n = ...)` to see more rows
> parameters
# A tibble: 80 × 3
b0s b1s msr
<dbl> <dbl> <dbl>
1 0.791 0.0539 159.
2 0.729 0.439 107.
3 0.679 0.747 74.3
4 0.638 0.994 53.1
5 0.604 1.19 39.5
6 0.577 1.35 30.8
7 0.555 1.48 25.3
8 0.538 1.58 21.7
9 0.523 1.66 19.4
10 0.511 1.72 18.0
# ℹ 70 more rows
# ℹ Use `print(n = ...)` to see more rows
>
>