아래 문서를 보시오.
sampling distribution
sampling distribution in r
central limit theorem

• 어떤 모집단이 존재한다.
• 모집단의 분포는 정상분포일 필요가 없다.
• 이 집단에서 무작위 샘플을 무한히 (많은 숫자만큼) 취하여 샘플의 평균을 기록하면
  • 이 샘플평균들은 정상분포의 곡선을 보인다.
  • 이 샘플평균들의 평균은 모집단의 평균이 된다.
  • 이 샘플평균들의 분산값은 $\dfrac{\sigma^{2}}{n}$을 갖는다.

이를 하나의 식으로 요약하자면 (확률과통계 시간에서 배운)

$ \overline{X} \sim \text{N} \left(\mu, \dfrac{\sigma^2}{n} \right)$

예,

p <- c(0,1,2,3,4,5,6,7,8,9)
set.seed(512)
iter <- 10000
n <- 2
means <- rep (NA, iter)
for(i in 1:iter){
    means[i] = mean(sample(p, n))
}
mean(means)
var(means)
sd(means)
mean(p)
var(p)/n
sd(p)/sqrt(n)
sd1 <- sd(means)
m <- mean(means)
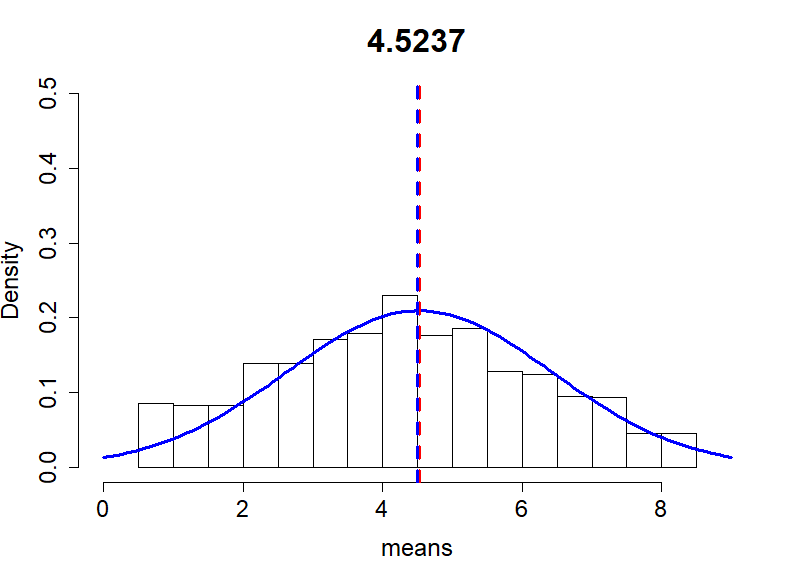
hist(means, main=m, xlim=c(0,9), ylim=c(0,0.5), 
     freq = F, 
     cex.main=2, cex.axis=1.5, cex.lab = 1.5)
curve(dnorm(x, mean=m, sd=sd1), col="blue", 
      add=TRUE, lty=1, lwd=3)
abline(v = m, lty=2, lwd=3, col="red")
abline(v=mean(p), lty=2, lwd=3, col="blue")

set.seed(512)
par(mfrow=c(2,2))
n <- 3
means <- rep (NA, iter)
for(i in 1:iter){
    means[i] = mean(sample(p, n))
}
mean(means)
var(means)
sd(means)
mean(p)
var(p)/n
sd(p)/sqrt(n)
sd1 <- sd(means)
m <- mean(means)
hist(means, main=m, xlim=c(0,9), ylim=c(0,0.5), 
     freq = F, 
     cex.main=2, cex.axis=1.5, cex.lab = 1.5)
curve(dnorm(x, mean=m, sd=sd1), col="blue", 
      add=TRUE, lty=1, lwd=3)
abline(v = m, lty=2, lwd=3, col="red")
abline(v=mean(p), lty=2, lwd=3, col="blue")

n <- 4
means <- rep (NA, iter)
for(i in 1:iter){
    means[i] = mean(sample(p, n))
}
mean(means)
var(means)
sd(means)
mean(p)
var(p)/n
sd(p)/sqrt(n)
sd1 <- sd(means)
m <- mean(means)
hist(means, main=m, xlim=c(0,9), ylim=c(0,0.5), 
     freq = F, 
     cex.main=2, cex.axis=1.5, cex.lab = 1.5)
curve(dnorm(x, mean=m, sd=sd1), col="blue", 
      add=TRUE, lty=1, lwd=3)
abline(v = m, lty=2, lwd=3, col="red")
abline(v=mean(p), lty=2, lwd=3, col="blue")

n <- 5
means <- rep (NA, iter)
for(i in 1:iter){
    means[i] = mean(sample(p, n))
}
mean(means)
var(means)
sd(means)
mean(p)
var(p)/n
sd(p)/sqrt(n)
sd1 <- sd(means)
m <- mean(means)
hist(means, main=m, xlim=c(0,9), ylim=c(0,0.5), 
     freq = F, 
     cex.main=2, cex.axis=1.5, cex.lab = 1.5)
curve(dnorm(x, mean=m, sd=sd1), col="blue", 
      add=TRUE, lty=1, lwd=3)
abline(v = m, lty=2, lwd=3, col="red")
abline(v=mean(p), lty=2, lwd=3, col="blue")

n <- 6
means <- rep (NA, iter)
for(i in 1:iter){
    means[i] = mean(sample(p, n))
}
mean(means)
var(means)
sd(means)
mean(p)
var(p)/n
sd(p)/sqrt(n)
sd1 <- sd(means)
m <- mean(means)
hist(means, main=m, xlim=c(0,9), ylim=c(0,0.5), 
     freq = F, 
     cex.main=2, cex.axis=1.5, cex.lab = 1.5)
curve(dnorm(x, mean=m, sd=sd1), col="blue", 
      add=TRUE, lty=1, lwd=3)
abline(v = m, lty=2, lwd=3, col="red")
abline(v=mean(p), lty=2, lwd=3, col="blue")

par(mfrow=c(1,1))

이 것이 의미하는 것은

• 모집단의 평균 = 4.5
• 모집단의 분산값 = 9.166667
• 표준편차 = 3.02765

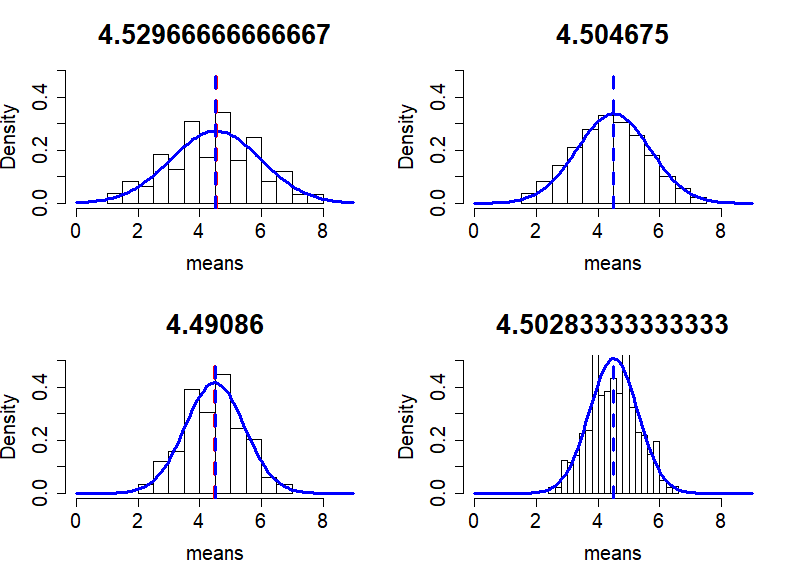
• n = 3,
  • mean = 4.5059
  • var = 2.178116
• n = 4,
  • mean = 4.509225
  • var = 1.377784
• n = 5,
  • mean = 4.49568
  • var = 0.9313945
• n = 6,
  • mean = 4.485983
  • var = 0.610484

위와 비슷하지만 다른 수준의 측정 예.

아주대학교 학생의 온라인 수업에 대한 찬성과 반대가 50 대 50이라고 하자. 그러나, 당신은 이를 알고 있지 못하다. 이를 알아보기 위해서 n = 100 명의 샘플을 무한히 취해서 찬성의 퍼센티지를 알아보려 한다면, 진짜 평균인 50%를 중심으로 그 평균이 모일 것이다. 이는 위에서 언급한 것과 마찬가지로 전체 평균인 50%를 중심으로 그 평균이 모이는 것과 같다. 이 때, 그 표준편차는 아래와 같다.

$ s = \sqrt{\dfrac{p * q}{n}} \;\; \text{, where } \;\;\; q = 1 - p $

따라서 n = 100 일 때, 찬성 샘플 퍼센티지 분포의 표준편차인 표준오차값은

> se <- sqrt((0.5*0.5)/100)
> 2*se
[1] 0.1
> 

위를 이용해서 우리는 n=100 인 샘플의 찬성률은 진짜 찬성률은 50 % +- 10 %인 40-60 %에서 나타날 것을 알 수 있다. 만약에 n = 100이 아닌 1600이라면 50 +- 2.5 인 47.5 - 52.5 % 임을 알 수 있다.

> se <- sqrt((0.5*0.5)/1600)
> 2*se
[1] 0.025
> 

그런데, 위는 모집단의 분포를 알고 있고, 샘플을 취했을 때, 그 샘플의 평균이 (여기서는 퍼센티지) 나타날 구간을 예측하는 것이다. 그러나, 현실에서는 대부분 그 모집단의 특성을 (파라미터를) 알지 못한다. 오히려, 대개는 하나의 샘플을 취해서 그 샘플을 가지고 모집단의 퍼센티지를 예측한다. 이 경우, 우리는

$ s = \sqrt{\dfrac{\hat{p} * \hat{q}}{n}} \;\; \text{, where } \;\;\; \hat{q} = 1 - \hat{p} $

이 논리는 분자부분이 probability sampling을 취했다면 약간의 오차라도 큰 차이가 나지 않을 것이며, n이 충분히 크면, se 값이 충분히 작을 것이라는 논리이다.