This is an old revision of the document!
Table of Contents
정보의 시각화: 첫인상
Charts
- 모은 데이터를 분석하는 한 방법
- 상황을 파악하고 결론을 내려 결정을 (decision making) 할 수 있도록 한다.
- 그러나, 데이터의 시각화에는 많은 허점이 따른다.
- the same data
- different axis
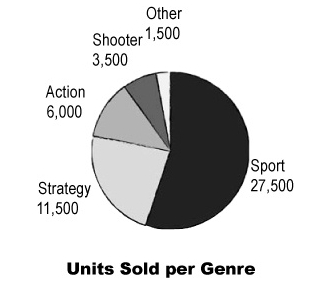
Pie Chart
Good to go with
- frequency data for categories which should add up to 100 percent
- side note for actual numbers and
- table
- 각 게임 장르별 사용자의 만족도 퍼센티지를 모아 놓은 파이차트는 유용하지 않다.
Bar chart
Histogram
| ser | freq |
|---|---|
| 1 | 100 |
| 2 | 88 |
| 3 | 159 |
| 4 | 201 |
| 5 | 250 |
| 6 | 250 |
| 7 | 254 |
| 8 | 288 |
| 9 | 356 |
| 10 | 380 |
| 11 | 430 |
| 12 | 450 |
| 13 | 433 |
| 14 | 543 |
| 15 | 540 |
| 16 | 570 |
| 17 | 450 |
| 18 | 433 |
| 19 | 543 |
| 20 | 690 |
| 21 | 640 |
| 22 | 720 |
| 23 | 777 |
| 24 | 720 |
| 25 | 880 |
| 26 | 900 |
Excel에서의 histogram
| Bin | Frequency |
| 199 | 3 |
| 399 | 7 |
| 599 | 9 |
| 799 | 5 |
| 999 | 2 |
in R . . . .
dat <- c(100, 88, 159, 201, 250, 250, 254, 288, 356, 380,
430, 450, 433, 543, 540, 570, 450, 433, 543, 690,
640, 720, 777, 720, 880, 900)
dat
hist(dat)
hist(dat, breaks=5)
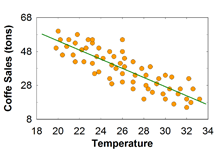
Scatter plot
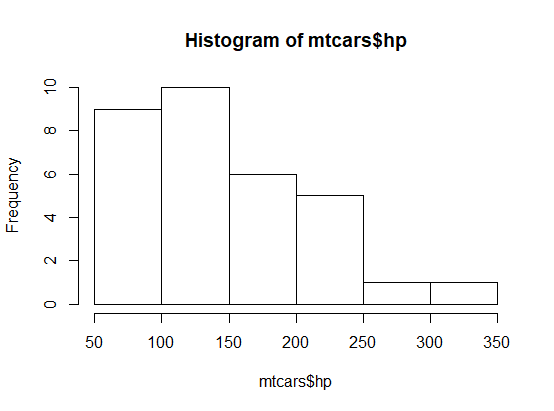
hist(mtcars$hp)
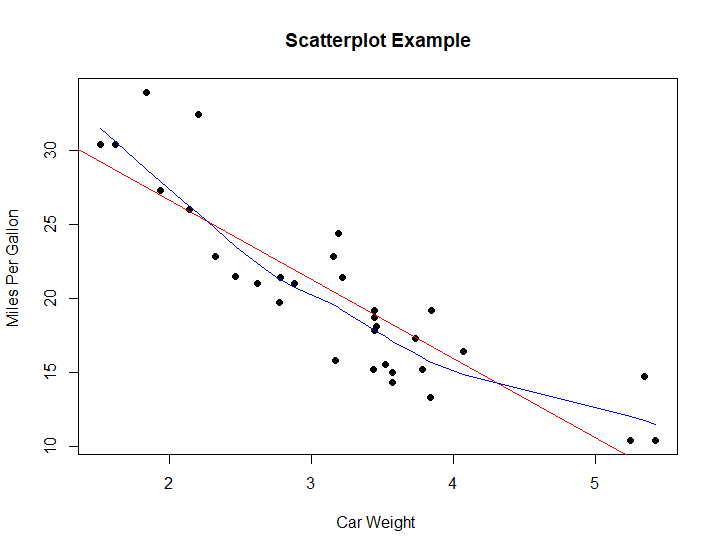
# Simple Scatterplot attach(mtcars) plot(wt, mpg, main="Scatterplot Example", xlab="Car Weight ", ylab="Miles Per Gallon ", pch=19)
explanatory (설명) variable at x axis
response (반응) at y axis
But, it does mean no causal relationship between the two variables. Association between two does not guarantee a causal relationship.
Drawing a line among the data.
# Add fit lines abline(lm(mpg~wt), col="red") # regression line (y~x) lines(lowess(wt,mpg), col="blue") # lowess line (x,y)
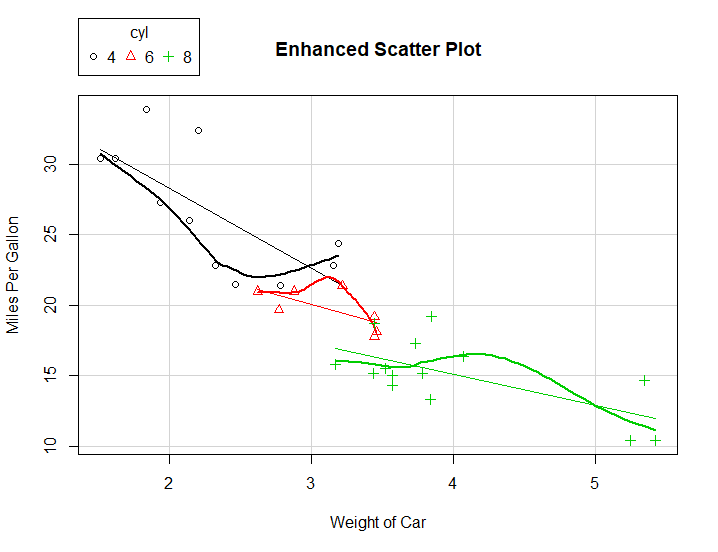
A bit more fancy line
# Enhanced Scatterplot of MPG vs. Weight # by Number of Car Cylinders library(car) scatterplot(mpg ~ wt | cyl, data=mtcars, xlab="Weight of Car", ylab="Miles Per Gallon", main="Enhanced Scatter Plot", labels=row.names(mtcars))
Line can be:
관계의 방향 (direction)
관계의 모양 (shape)
관계의 정도 (힘)
Pearson's r 의 의미
Relations, not cause-effect
상관관계 계수는 단순히 두 변인 (x, y) 간의 관계가 있다는 것을 알려줄 뿐, 왜 그 관계가 있는지는 설명하지 않는다. 바꿔 말하면, 충분한 r 값을 구했다고 해서 이 값이 두 변인 간의 '원인'과 '결과'의 관계를 말한다고 이야기 하면 안된다. 예를 들면 아이스크림의 판매량과 성범죄가 서로 상관관계에 있다고 해서, 전자가 후자의 원인이라고 단정할 수 있는 근거는 없다. 이는 연구자의 논리적인 판단 혹은 이론적인 판단에 따른다.
Interpretation with limited range
데이터의 Range에 대한 판단에 신중해야 한다. 왜냐 하면, 데이터의 어느 곳을 자르느냐에 따라서 r 값이 심하게 변하기 때문이다.
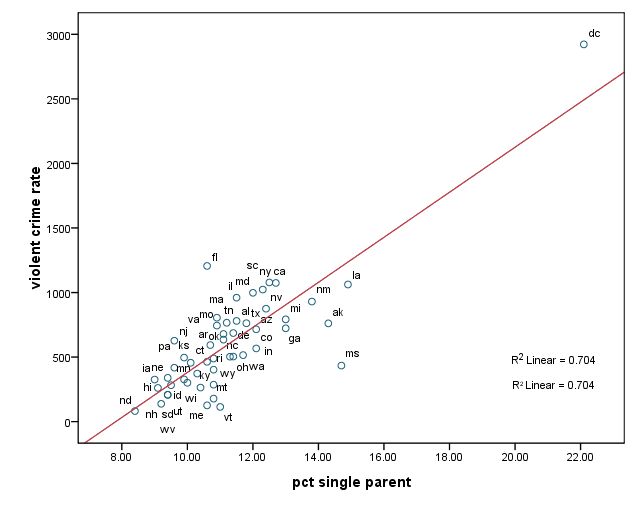
Outliers
위의 설명과 관련하여, 만약에 아주 심한 Outlier가 존재한다면 두 변인 간의 상관관계에 심한 영향을 준다.
make it sure that there is no data entry error.
see
https://www.gapminder.org/answers/how-does-income-relate-to-life-expectancy/
- Life expectancy data: life.exp.csv
le <- as.data.frame(read.csv("http://commres.net/wiki/_media/life.exp.csv", header=T))
colnames(le)[1] <- "c.code" # not really necessary. But, sometimes imported first characters are broken.
lea <- le$X2017
leb <- lea[complete.cases(lea)]
hist(leb, color="grey")
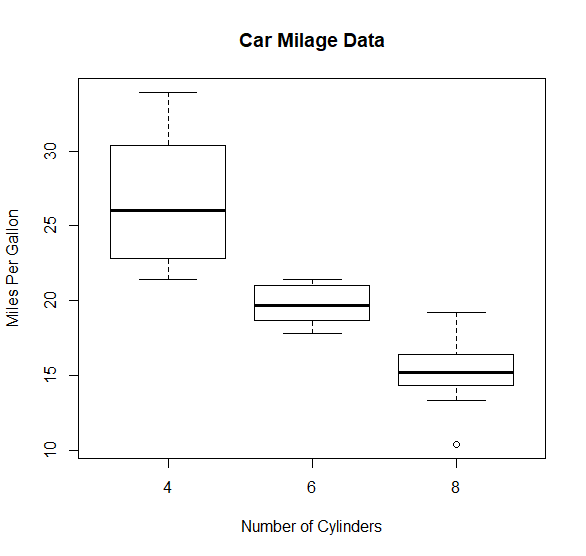
box plot
# Boxplot of MPG by Car Cylinders
boxplot(mpg~cyl,data=mtcars,
main="Car Milage Data",
xlab="Number of Cylinders",
ylab="Miles Per Gallon")