This is an old revision of the document!
Table of Contents
Look at the evidence
Miracle drug: SnoreCull cures 90% of snores within 2 weeks.
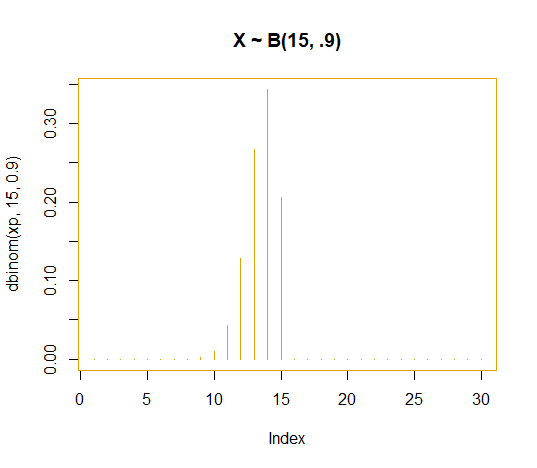
n = 15
| Cured? | Yes | No |
| Frequency | 11 | 4 |
If the drug cures 90% of people, how many people in the sample of 15 snorers would you expect to have been cured? What sort of distribution do you think this follows?
A: 제약회사의 말이 맞다면 .9 (90%) 치료율을 보여야 하기 때문에, 15명의 .9인 13.5명, 이를 반올림한 14명이 치료되어야 한다. 그런데, 이번 샘플에서의 치료된 환자의 숫자는 11이었다. 이를 어떻게 해석하고 판단해야 하는가?
X 는 B (15, 0.9)의 distribution 을 따른다.
위의 결과를 가지고 약의 효력가 (효과) 있다고 할 수 있는가?
Step 1: Decide on the hypothesis
Null Hypothesis $H_{0}: P = .9$
- 제약회사의 말이 맞다고 가정하는 것을 말한다. 즉, 치료율이 90%이다.
Alternative Hypothesis $H_{1}: P < .9 $
- 위의 말을 부정하는 것이다. 혹은 내가 진정 밝히고자하는 문제이라고 할 수 있다 – “제약회사는 거짓말을 하고 있다.”
- 이에 따라서 $H_{1}: P \le .9 $ 라고 보아도 된다 (two tale)
Step 2: Choose your test statistic

X는 위의 분포를 따른다는 것을 영가설을 이용하여 인지한다. 그리고 이 분포를 따를 때 $P(X \le 11)$의 확률이 무엇일까를 보는 문제이다. 그 기준을 0.05로 잡고, 이 기준보다 안쪽에 있으면 normal하게 나타나는 확률로 인정하기로, 또 반대로 바깥쪽에 (더 작은 쪽에) 있으면, normal하지 않은 것으로 판단하기로 한다. Normal하지 않다는 것이 의미하는 것은 11번이 15번 시동 중 (trial 중) 0.9의 성공률을 가지는 분포에서 less likely 즉, normal하지 않게 나타난다는 뜻이므로 이는 영가설을 부정하는 것이다.
Step 3: Determine the critical region

위의 그림에서: “그렇다면 어는 수준까지 (몇 명까지) 떨어져야 (치료된 사람이 적어야), 90%에 미치지 못한다고 하겠는가? 숫자상으로는 13.5명이지만 13명이라도 90%에 미치는 수준이라고 판단해야 할까?라고 생각한다면, 어디까지 떨어지면 90%가 아닌것을 확신할 수 있을까? 12명? 11명? 10명? 9명?
즉, 어느 지점에서 제약회사의 주장을 기각해야 할까?
유의수준을 (confidence interval) 정하여 기각할 지점을 찾는다.
이를 5%로 정하면 (혹은 95%) –
이번에 구한 치료된 11명이 이 5%에 해당되는 숫자인지 아니면 95%에 해당되는 숫자인지 본다.
xp <- c(1:30) plot(dbinom(xp, 15, .9), type = "hist")
To find the critical region, first decide on the significance level
alpha = .05
p level = .05
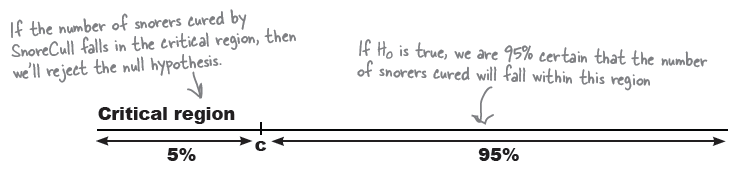
즉, $X \sim B(15, 0.9)$를 따를 때, $P(X \le 11)$ 일 때의 확률이 무엇인가를 보아서 이것이 0.05보다 작으면 영가설을 기각한다.
Step 4: Find the p-value
위에서 살펴본 것처럼:
$X \sim B(15, 0.9)$ 에서 $P(X \le 11)$은 무엇인지를 본다.
pbinom(11, 15, 0.9)
> pbinom(11,15,.9) [1] 0.05555563
0.05555563 값은 (P값) 0.05 범위 밖에 위치하므로 영가설을 기각하지 못한다. 즉, 회사의 claim을 기각하지 못하고 받아들인다.

We accept the claims of the drug company
> ############ > pbinom(11, 15, .9) # 11명 이하로 나은 수 있는 확률은 아래 점수와 같다 [1] 0.05555563 > pbinom(10, 15, .9) # 10명 이하라고 하면 그 때의 확률은 0.05보다 # 작은 0.012 이고, 이것의 의미는 사건이 일어날 # 확률이 (나을 확률이) 일어나기 극히 어려운 경우 # 임을 말한다 (1/20보다 작은 확률이라는 뜻) [1] 0.01272048 >
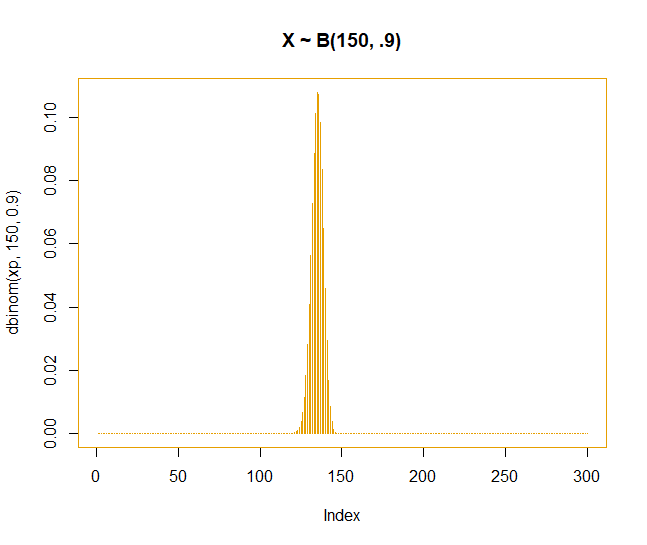
What if the sample size gets larger
| Cured? | yes | no |
| Freq | 110 | 40 |
Null H : P = 0.9
Alt H: P < 0.9
xp <- c(1:300) plot(dbinom(xp, 150, .9), type = "hist", main = "X ~ B(150, .9)")
pbinom(110, 150, .9)
> pbinom(110, 150, .9) [1] 5.785159e-09
textbook —-
| Cured? | yes | no |
| Freq | 80 | 20 |
Null H : P = 0.9
Alt H: P < 0.9
이 때의 Distribution은 Binomial이므로
$X \sim B(100, 0.9)$ 를 따를 것이고, 이 때의 $P(X \le 80)$ 경우를 살펴보고 이것이 critical value (alpha)인 .05를 기준으로 어디에 위치하는지를 살펴본다.
그런데, 위를 손으로 계산하는 것은 무리이다. 참고로 R에서는
> pbinom(80, 100, .9) [1] 0.001978561
- np > 5, nq > 5, 인 경우에 해당하므로
- $X \sim N(\mu, \sigma^{2})$ 인 경우에 $\overline{X}$는 $X \sim N(\mu, \frac{\sigma^{2}}{n})$ 이다.
- 즉, 샘플사이즈가 충분히 크면, 샘플 평균의 분포는 $X \sim N(\mu, \frac{\sigma^{2}}{n})$ 를 따른다.
- 만약에 모집단의 분산을 모른다면 샘플의 분산을 이용한다. 즉, $X \sim N(\mu, \frac{s^{2}}{n})$
- 또한 샘플의 크기가 비교적 작다면 t-distribution을 상정하고 그 값을 구한다.
$X \sim B (100, .9)$ 에서, $E(X) = np$, $V(X) = npq$일 것이다.
따라서, $E(X) = 90$, $V(X) = 9$ 이므로
$X \sim B (100, .9)$ 는 $X \sim N(np, npq)$, 즉, $X \sim N(90, 9)$ 를 따르는 분포를 보일 것이다.
그런데, n=100의 샘플평균들의 분포는 $X \sim N(90, 9/100)$ 이고 이때 se = 0.3 이다.
이 때
X = 80 이었으므로 이 지점의 Z score는
\begin{eqnarray*}
z & = & \dfrac{X-90}{sd} \\
& = & \dfrac{80-90}{0.3} \\
& = & -0.333 \\
\end{eqnarray*}
z = -3.33 일 때의 Probability는 .0004이다. 이는 .05보다 훨씬 바깥 쪽에 위치하므로
Null hypothesis를 부정한다.
> pnorm(-3.33, 0, 1) [1] 0.0004342299
그런데 보통은 (r을 사용하지 않을 경우에는) 위와 같은 계산이 어려우므로,
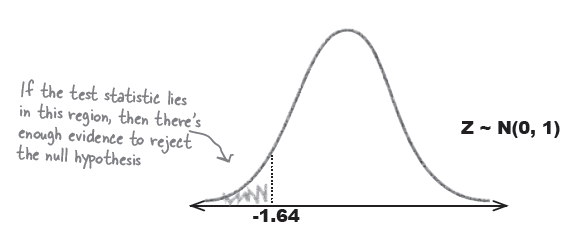
z 점수가 .05일 경우의 점수를 찾아 본다 (z-table에서). 이 때의 z 값은 -1.64 이므로 이 점수와 -3.33을 비교한다. 위의 그림처럼 -3.33은 영가설 기각기준 왼 쪽에 존재하므로 영가설을 부정 혹은 기각한다.
즉, 회사의 claim 인 90% cure를 받아들이지 못한다.