This is an old revision of the document!
Table of Contents
Look at the evidence
Miracle drug: SnoreCull cures 90% of snores within 2 weeks.
n = 15
| Cured? | Yes | No |
| Frequency | 11 | 4 |
If the drug cures 90% of people, how many people in the sample of 15 snorers would you expect to have been cured? What sort of distribution do you think this follows?
X 는 B (15, 0.9)의 distribution 을 따른다.
위의 결과를 가지고 약의 효력가 (효과) 있다고 할 수 있는가?
Step 1: Decide on the hypothesis
Null H: P = .9
Alt H: P < .9 or $P \ne .9$
Step 2: Choose your test statistic

X는 위의 분포를 따른다는 것을 영가설을 이용하여 인지한다. 그리고 이 분포를 따를 때 $P(X \le 11)$의 확률이 무엇일까를 보는 문제이다. 그 기준을 0.05로 잡고, 이 기준보다 안쪽에 있으면 normal하게 나타나는 확률로 인정하기로, 또 반대로 바깥쪽에 (더 작은 쪽에) 있으면, normal하지 않은 것으로 판단하기로 한다. Normal하지 않다는 것이 의미하는 것은 11번이 15번 시동 중 (trial 중) 0.9의 성공률을 가지는 분포에서 less likely 즉, normal하지 않게 나타난다는 뜻이므로 이는 영가설을 부정하는 것이다.
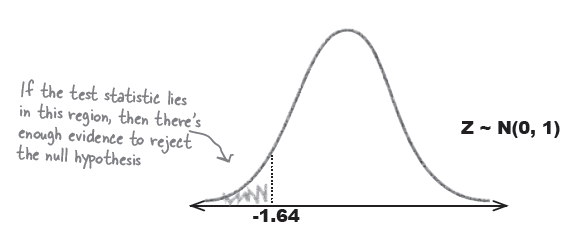
Step 3: Determine the critical region
xp <- c(1:30) plot(dbinom(xp, 15, .9), type = "hist")
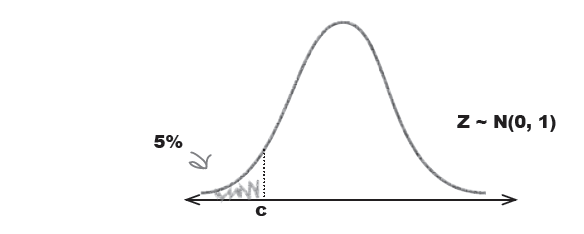
To find the critical region, first decide on the significance level
alpha = .05
p level = .05
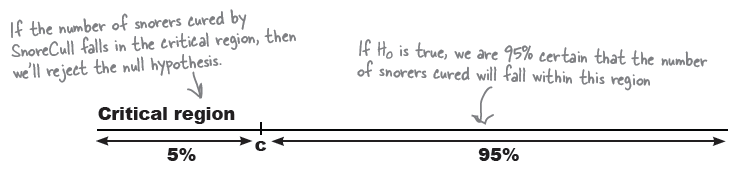
즉, $X \sim B(15, 0.9)$를 따를 때, $P(X \le 11)$ 일 때의 확률이 무엇인가를 보아서 이것이 0.05보다 작으면 영가설을 기각한다.
Step 4: Find the p-value
위에서 살펴본 것처럼:
$X \sim B(15, 0.9)$ 에서 $P(X \le 11)$은 무엇인지를 본다.
pnorm(11, 15, 0.9)
> pbinom(11,15,.9) [1] 0.05555563
0.05555563 값은 (P값) 0.05 범위 밖에 위치하므로 영가설을 기각하지 못한다. 즉, 회사의 claim을 기각하지 못하고 받아들인다.

We accept the claims of the drug company
What if the sample size gets larger
| Cured? | yes | no |
| Freq | 80 | 20 |
Null H : P = 0.9
Alt H: P < 0.9
이 때의 Distribution은 Binomial이므로
$X \sim B(100, 0.9)$ 를 따를 것이고, 이 때의 $P(X \le 80)$ 경우를 살펴보고 이것이 critical value (alpha)인 .05를 기준으로 어디에 위치하는지를 살펴본다.
그런데, 위를 손으로 계산하는 것은 무리이다. 참고로 R에서는
> pbinom(80,100,.9) [1] 0.001978561
- np > 5, nq > 5, 인 경우에 해당하므로
- $X \sim N(\mu, \sigma^{2})$ 인 경우에 $\overline{X}$는 $X \sim N(\mu, \frac{\sigma^{2}}{n})$ 이다.
- 즉, 샘플사이즈가 충분히 크면, 샘플 평균의 분포는 $X \sim N(\mu, \frac{\sigma^{2}}{n})$ 를 따른다.
- 만약에 모집단의 분산을 모른다면 샘플의 분산을 이용한다. 즉, $X \sim N(\mu, \frac{s^{2}}{n})$
- 또한 샘플의 크기가 비교적 작다면 t-distribution을 상정하고 그 값을 구한다.
$X ~ N(90, np)$
$X ~ N(90, 9)$
X =80 일 때의 Z score는
\begin{eqnarray*}
z & = & \dfrac{X-90}{sd} \\
& = & \dfrac{80-90}{3} \\
& = & -3.33 \\
\end{eqnarray*}
z = -3.33 일 때의 Probability는 .0004이다. 이는 .05보다 훨씬 바깥 쪽에 위치하므로
Null hypothesis를 부정한다.
즉, 회사의 claim 인 90% cure를 받아들이지 못한다.