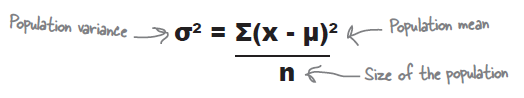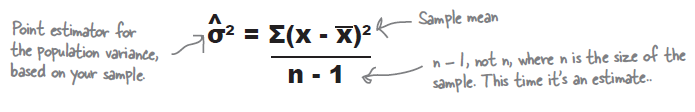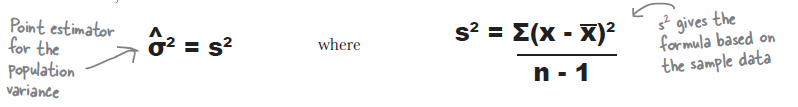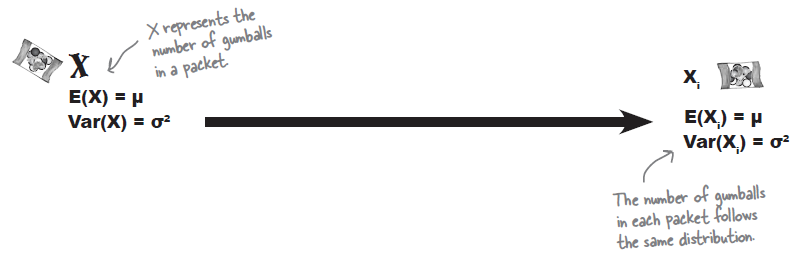This is an old revision of the document!
Table of Contents
Estimating Populations and Samples: Making Predictions
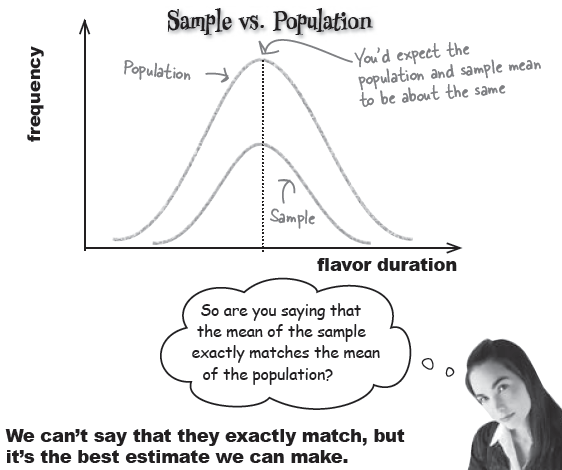
So how can we use the results of the sample taste test to tell us the mean amount of time gumball flavor lasts for in the general gumball population?
The answer is actually pretty intuitive. We assume that the mean flavor duration of the gumballs in the sample matches that of the population. In other words, we find the mean of the sample and use it as the mean for the population too.
Here's a sketch showing the distribution of the sample, and what you’d expect the distribution of the population to look like based on the sample. You’d expect the distribution of the population to be a similar shape to that of the sample, so you can assume that the mean of the sample and population have about the same value.
$$\mu \quad \quad \hat\mu$$
$\hat\mu$ : See this hat I’m wearing? It means I’m a point estimator. If you don’t have the exact value of the mean, then I'm the next best thing.
$\hat{Y}$, $\hat{\mu}$ 등의 사인은 대개 estimates를 의미한다 (예측치 혹은 추정치).
\begin{align*} \overline{X} & = \frac {\sum{X}}{n} \\ & = \frac{ \sum_{i=1}^{n} X_{i} } {n} \\ & = \hat{\mu} \end{align*}
Estimating population variance
 | There are fewer values in the sample, so there’s a good chance that more extreme values will be excluded. |
 |
|
\begin{eqnarray*} \sigma^{2} & = & \frac{\sum(X-\mu)^2}{n} \end{eqnarray*}
\begin{eqnarray*} \hat{\sigma^{2}} & = & \frac{\sum(X-\overline{X})^2}{n-1} \end{eqnarray*}
\begin{eqnarray*} \hat{\sigma^{2}} & = & s^2 \\ s^2 & = & \frac {\sum(X-\overline{X})^2}{n-1} \end{eqnarray*}
x <- c(61.9, 62.6, 63.3, 64.8, 65.1, 66.4, 67.1, 67.2, 68.7, 69.9) mean(x) var(x)
> x <- c(61.9, 62.6, 63.3, 64.8, 65.1, 66.4, 67.1, 67.2, 68.7, 69.9) > mean(x) [1] 65.7 > var(x) [1] 6.924444 >
| x | mean | x - mean | ds^2 |
| 61.9 | 65.7 | -3.8 | 14.44 |
| 62.6 | 65.7 | -3.1 | 9.61 |
| 63.3 | 65.7 | -2.4 | 5.76 |
| 64.8 | 65.7 | -0.9 | 0.81 |
| 65.1 | 65.7 | -0.6 | 0.36 |
| 66.4 | 65.7 | 0.7 | 0.49 |
| 67.1 | 65.7 | 1.4 | 1.96 |
| 67.2 | 65.7 | 1.5 | 2.25 |
| 68.7 | 65.7 | 3 | 9 |
| 69.9 | 65.7 | 4.2 | 17.64 |
| $\sum{ds^2}$ | 62.32 | ||
| $n-1$ | 9 | ||
| $Var(x)$ | 6.924444 |
Estimating proportion
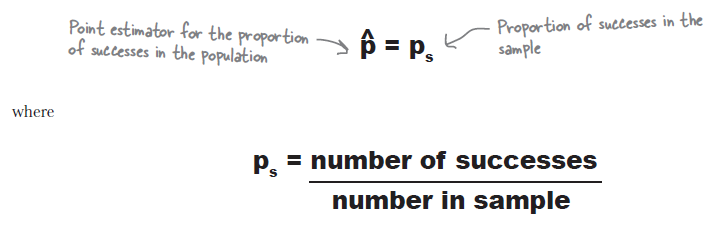
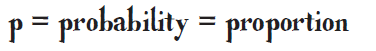
Or
\begin{eqnarray*}
\Large{P_{s}} & = & \Large{\frac{\text{number of the same kind}}{\text{number in sample}}}
\end{eqnarray*}
p = 32/40 = 0.8
Mighty Gumball takes another sample of their super-long-lasting gumballs, and finds that in the sample, 10 out of 40 people prefer the pink gumballs to all other colors. What proportion of people prefer pink gumballs in the population? What’s the probability of choosing someone from the population who doesn’t prefer pink gumballs?
핑크풍선검을 선호하는 사람의 비율
\begin{eqnarray*}
\hat{P} = P_{s} & = & \frac {10}{40} \\
& = & 0.25
\end{eqnarray*}
핑크가 아닌 풍선검을 선호하는 사람의 비율
\begin{eqnarray*}
\hat{P} = P_{s'} & = & 1 - \hat{P} \\
& = & 1 - 0.25 \\
& = & 0.75
\end{eqnarray*}
Sampling distribution of proportions
Expectation of samples proportions (Ps)
red gumballs in the population = 0.25
A jumbo box of gumballs containing 100 gumballs (n = 100).
What is the probability to get 40 red balls out of a box?
X는 $X \sim B(100, 1/4)$ 의 분포를 따를 때, P(X=40)?
> dbinom(40, 100, 1/4) [1] 0.0003626268
population: gumball의 25%가 red라고 할 때,
하나의 샘플을 뽑는다고 가정할 때의 기대값과 분산값은 무엇인가?
Bernoulli distribution에 따르면,
하나의 검볼을 뽑을 때, 이것이 red인지 아닌지에 대한 기대값과 분산값은
output = 1(red), 0(not-red)
\begin{eqnarray*} E(Y) & = & p = 1/4 \\ Var(Y) & = & p * q = 3/16 \end{eqnarray*}
위의 상황에서 100번 independent trial을 통해서 구한 평균과 분산값은:
$X \sim B(100, 1/4)$의 분포를 따른다고 할 때,
혹은 위의 분포는 이항분포이므로 $X ~ B(n, p)$ 에서 $E(X) = np$; $V(X) = npq$ 이다.
\begin{eqnarray*} E(X) & = & n * p = 100 * 1/4 = 25 \\ Var(X) & = & n * p * q = 100 * 1/4 * 3/4 = 18.75 \end{eqnarray*}
위와 같이 $n = 100$ 일때 각각의 시도에서의 (trial) proportion 값은 ($\hat{P}$), 즉
\begin{eqnarray*}
X_{i} & = & \text{the number of red gumball,} \\
n & = & 100
\end{eqnarray*} 조건에서의 proportion (비율) 값은
\begin{eqnarray*}
\hat{P_{1}} & = \frac{X_{1}}{n} = 0.34, (X_{1} = 34) \\
\hat{P_{2}} & = \frac{X_{2}}{n} = 0.23, (X_{2} = 23) \\
\hat{P_{3}} & = \frac{X_{3}}{n} = 0.22, (X_{3} = 22) \\
\hat{P_{4}} & = \frac{X_{4}}{n} = 0.21, (X_{4} = 21) \\
& \cdots \cdots \cdots \cdots \cdots \\
\hat{P_{k}} & = \frac{X_{k}}{n} = 0.24, (X_{k} = 24) \\
\end{eqnarray*}
즉, $X \sim B(n, p)$ 일 때, sample의 비율은 $P_{s} = \dfrac{X}{n}$를 따른다 ($X$ = red gumball이 나온 갯수, $n$ = sample 크기).
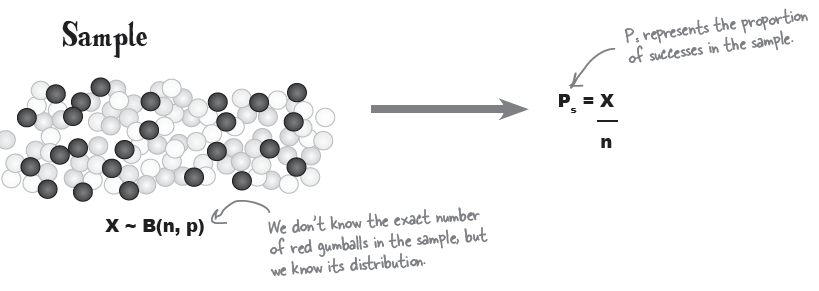
위의 sampling을 계속한다면 아래 그림과 같은 결과를 의미한다.
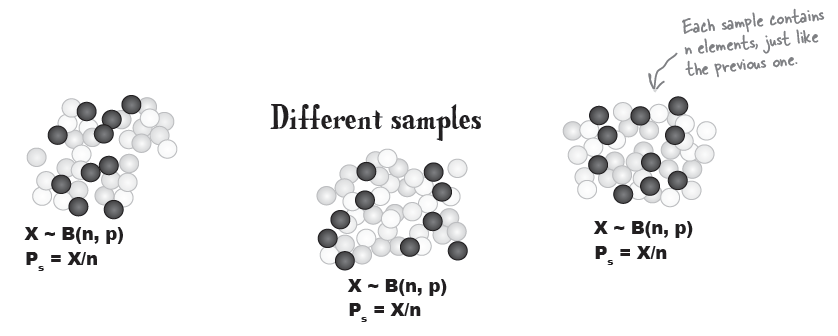
이렇게 계속 샘플링을 하여 얻은 비율의 $P_{s}$ 기댓값을 ($E(P_{s})$) 구한다고 하면;
\begin{eqnarray*} E(\text{probability of samples}) & = & E(P_{s}) \\ & = & E \left(\frac{X}{n} \right) \\ & = & \frac{E(X)}{n} \\ & = & \frac{np}{n} \\ & = & p \end{eqnarray*}
아래는 위의 시뮬레이션이다.
- $X ~ B(100, 1/4)$의 이항분포에서 (n=100, p=1/4)
- random 하게 1000번의 (k=1000) 샘플링을 해서
- 얻는 Red gumball의 숫자
> set.seed(101) > k <- 1000 > n <- 100 > p <- 1/4 > q <- 1-p # in order to clarify what we are doing # X~B(n,p) 일 때, 100개의 검볼을 샘플링해서 # red gumball을 세봤더니 > rbinom(1,n,p) # 24개 였다라는 뜻 [1] 24 # 아래는 이것을 1000번 (k번) 한 것 > numbers.of.red.gumball <- rbinom(k, n, p) > numbers.of.red.gumball [1] 18 27 27 22 23 26 23 26 25 30 27 28 32 24 26 29 22 24 18 27 33 22 27 31 29 19 [27] 24 24 27 24 23 21 21 25 31 21 29 16 31 24 24 28 23 24 22 19 31 28 20 19 24 27 [53] 28 24 28 27 25 27 26 29 29 26 36 29 27 16 23 30 32 22 32 26 29 29 22 18 22 27 [79] 33 27 28 28 34 15 32 23 24 20 16 27 31 27 21 22 29 24 22 19 18 20 17 24 30 27 [105] 23 19 17 28 37 20 18 26 30 30 34 30 25 23 26 24 20 19 25 22 29 25 25 27 19 27 [131] 23 22 23 26 25 25 32 25 27 32 22 32 23 30 21 25 27 17 24 21 24 26 33 20 22 26 [157] 28 25 30 33 27 30 26 23 39 23 31 18 26 27 34 25 28 31 35 28 29 32 27 31 28 25 [183] 22 23 15 22 20 26 21 22 16 23 22 31 24 27 31 21 24 26 26 22 22 34 19 30 22 28 [209] 25 24 29 25 25 16 27 23 25 32 18 22 25 25 24 24 21 32 20 28 29 22 23 22 25 21 [235] 27 22 24 29 24 22 30 22 21 17 25 23 21 27 22 22 25 22 29 24 26 32 28 20 22 22 [261] 27 26 22 24 31 18 27 29 28 17 27 33 23 33 25 32 26 23 19 21 20 23 15 19 23 26 [287] 27 28 23 24 35 27 30 23 25 24 31 23 20 22 22 26 21 22 26 28 26 23 21 13 29 27 [313] 21 34 28 24 19 26 27 25 23 27 25 19 29 18 28 21 27 28 28 22 22 20 20 25 27 17 [339] 16 27 32 23 18 28 31 29 21 27 27 30 21 25 20 25 26 30 26 21 15 29 22 21 16 25 [365] 25 27 26 27 28 21 27 24 25 24 39 24 28 33 20 26 24 27 20 31 27 27 20 21 31 25 [391] 22 22 30 34 27 23 21 25 20 24 29 19 30 27 33 22 29 30 22 29 26 24 18 26 36 26 [417] 23 24 22 32 33 16 24 28 24 25 29 31 28 28 29 26 24 25 28 27 24 31 25 31 33 26 [443] 26 24 33 28 20 23 22 23 22 30 25 25 23 27 27 23 24 28 24 28 23 22 26 30 26 27 [469] 21 23 23 27 26 23 25 30 25 24 22 28 18 23 18 16 27 26 18 25 27 22 20 19 27 25 [495] 31 27 22 21 24 24 26 23 23 29 27 23 25 20 21 21 27 25 22 29 28 21 21 24 27 24 [521] 28 19 14 32 27 22 24 35 26 28 28 26 25 25 19 26 24 20 19 28 25 25 24 21 30 27 [547] 30 20 22 26 31 26 20 20 27 25 26 18 30 20 29 16 38 26 22 29 22 30 26 19 27 24 [573] 29 29 25 19 23 24 24 23 25 31 18 24 33 27 25 27 29 28 24 23 24 28 20 24 30 24 [599] 21 20 25 24 24 30 22 26 23 25 21 21 24 27 18 20 22 30 25 23 27 26 23 23 28 18 [625] 29 27 25 32 26 15 22 24 21 34 23 23 18 29 23 27 28 23 37 20 17 25 11 21 28 22 [651] 28 25 22 25 21 18 20 27 30 24 28 23 30 31 24 23 37 19 27 32 25 27 28 29 22 26 [677] 26 20 22 25 24 19 27 21 32 27 31 29 24 24 29 29 25 22 34 23 18 33 18 23 24 26 [703] 18 20 23 30 28 26 34 17 33 30 32 30 22 28 19 19 23 23 20 23 21 31 30 20 24 23 [729] 23 28 26 34 27 33 31 20 25 12 25 20 20 25 27 24 29 26 22 30 26 28 28 27 23 18 [755] 28 22 21 27 22 26 21 22 27 24 19 27 29 37 30 27 25 30 19 22 22 28 32 22 33 26 [781] 20 31 23 24 24 26 24 30 17 21 20 22 20 17 24 22 24 23 23 24 23 16 16 17 23 27 [807] 29 26 16 21 34 19 25 25 28 32 17 22 26 23 23 24 22 22 14 30 25 33 26 25 31 28 [833] 30 21 19 17 19 21 16 21 26 21 29 27 31 32 19 22 24 25 25 24 23 30 21 22 19 20 [859] 21 20 21 28 19 26 28 26 29 28 26 21 31 32 31 22 23 25 27 26 22 27 30 24 25 23 [885] 27 25 24 24 30 29 26 32 29 23 24 20 26 26 22 22 19 23 33 18 27 26 28 18 26 24 [911] 24 26 27 17 26 23 27 25 32 20 22 23 25 25 24 28 20 19 22 20 22 24 17 19 22 17 [937] 19 27 27 28 29 18 24 30 26 34 26 24 25 24 29 28 29 23 24 21 24 23 23 29 19 29 [963] 30 33 25 30 32 23 30 27 17 20 21 24 36 21 26 30 26 25 22 21 38 21 24 21 25 21 [989] 32 20 29 24 19 21 32 26 27 18 21 20 >
그런데 교재는 이 이항분포를 비율로 (proportion) 생각하므로, 같은 방식으로 Red gumball의 비율로 바꿔서 보면
> # 아래처럼 n으로 (100개의 검볼이 총 숫자이므로) > # 나눠주면 비율을 구할 수 있다 > proportions.of.rg <- numbers.of.red.gumball/n > ps.k <- proportions.of.rg > ps.k [1] 0.18 0.27 0.27 0.22 0.23 0.26 0.23 0.26 0.25 0.30 0.27 0.28 0.32 0.24 0.26 [16] 0.29 0.22 0.24 0.18 0.27 0.33 0.22 0.27 0.31 0.29 0.19 0.24 0.24 0.27 0.24 [31] 0.23 0.21 0.21 0.25 0.31 0.21 0.29 0.16 0.31 0.24 0.24 0.28 0.23 0.24 0.22 [46] 0.19 0.31 0.28 0.20 0.19 0.24 0.27 0.28 0.24 0.28 0.27 0.25 0.27 0.26 0.29 [61] 0.29 0.26 0.36 0.29 0.27 0.16 0.23 0.30 0.32 0.22 0.32 0.26 0.29 0.29 0.22 [76] 0.18 0.22 0.27 0.33 0.27 0.28 0.28 0.34 0.15 0.32 0.23 0.24 0.20 0.16 0.27 [91] 0.31 0.27 0.21 0.22 0.29 0.24 0.22 0.19 0.18 0.20 0.17 0.24 0.30 0.27 0.23 [106] 0.19 0.17 0.28 0.37 0.20 0.18 0.26 0.30 0.30 0.34 0.30 0.25 0.23 0.26 0.24 [121] 0.20 0.19 0.25 0.22 0.29 0.25 0.25 0.27 0.19 0.27 0.23 0.22 0.23 0.26 0.25 [136] 0.25 0.32 0.25 0.27 0.32 0.22 0.32 0.23 0.30 0.21 0.25 0.27 0.17 0.24 0.21 [151] 0.24 0.26 0.33 0.20 0.22 0.26 0.28 0.25 0.30 0.33 0.27 0.30 0.26 0.23 0.39 [166] 0.23 0.31 0.18 0.26 0.27 0.34 0.25 0.28 0.31 0.35 0.28 0.29 0.32 0.27 0.31 [181] 0.28 0.25 0.22 0.23 0.15 0.22 0.20 0.26 0.21 0.22 0.16 0.23 0.22 0.31 0.24 [196] 0.27 0.31 0.21 0.24 0.26 0.26 0.22 0.22 0.34 0.19 0.30 0.22 0.28 0.25 0.24 [211] 0.29 0.25 0.25 0.16 0.27 0.23 0.25 0.32 0.18 0.22 0.25 0.25 0.24 0.24 0.21 [226] 0.32 0.20 0.28 0.29 0.22 0.23 0.22 0.25 0.21 0.27 0.22 0.24 0.29 0.24 0.22 [241] 0.30 0.22 0.21 0.17 0.25 0.23 0.21 0.27 0.22 0.22 0.25 0.22 0.29 0.24 0.26 [256] 0.32 0.28 0.20 0.22 0.22 0.27 0.26 0.22 0.24 0.31 0.18 0.27 0.29 0.28 0.17 [271] 0.27 0.33 0.23 0.33 0.25 0.32 0.26 0.23 0.19 0.21 0.20 0.23 0.15 0.19 0.23 [286] 0.26 0.27 0.28 0.23 0.24 0.35 0.27 0.30 0.23 0.25 0.24 0.31 0.23 0.20 0.22 [301] 0.22 0.26 0.21 0.22 0.26 0.28 0.26 0.23 0.21 0.13 0.29 0.27 0.21 0.34 0.28 [316] 0.24 0.19 0.26 0.27 0.25 0.23 0.27 0.25 0.19 0.29 0.18 0.28 0.21 0.27 0.28 [331] 0.28 0.22 0.22 0.20 0.20 0.25 0.27 0.17 0.16 0.27 0.32 0.23 0.18 0.28 0.31 [346] 0.29 0.21 0.27 0.27 0.30 0.21 0.25 0.20 0.25 0.26 0.30 0.26 0.21 0.15 0.29 [361] 0.22 0.21 0.16 0.25 0.25 0.27 0.26 0.27 0.28 0.21 0.27 0.24 0.25 0.24 0.39 [376] 0.24 0.28 0.33 0.20 0.26 0.24 0.27 0.20 0.31 0.27 0.27 0.20 0.21 0.31 0.25 [391] 0.22 0.22 0.30 0.34 0.27 0.23 0.21 0.25 0.20 0.24 0.29 0.19 0.30 0.27 0.33 [406] 0.22 0.29 0.30 0.22 0.29 0.26 0.24 0.18 0.26 0.36 0.26 0.23 0.24 0.22 0.32 [421] 0.33 0.16 0.24 0.28 0.24 0.25 0.29 0.31 0.28 0.28 0.29 0.26 0.24 0.25 0.28 [436] 0.27 0.24 0.31 0.25 0.31 0.33 0.26 0.26 0.24 0.33 0.28 0.20 0.23 0.22 0.23 [451] 0.22 0.30 0.25 0.25 0.23 0.27 0.27 0.23 0.24 0.28 0.24 0.28 0.23 0.22 0.26 [466] 0.30 0.26 0.27 0.21 0.23 0.23 0.27 0.26 0.23 0.25 0.30 0.25 0.24 0.22 0.28 [481] 0.18 0.23 0.18 0.16 0.27 0.26 0.18 0.25 0.27 0.22 0.20 0.19 0.27 0.25 0.31 [496] 0.27 0.22 0.21 0.24 0.24 0.26 0.23 0.23 0.29 0.27 0.23 0.25 0.20 0.21 0.21 [511] 0.27 0.25 0.22 0.29 0.28 0.21 0.21 0.24 0.27 0.24 0.28 0.19 0.14 0.32 0.27 [526] 0.22 0.24 0.35 0.26 0.28 0.28 0.26 0.25 0.25 0.19 0.26 0.24 0.20 0.19 0.28 [541] 0.25 0.25 0.24 0.21 0.30 0.27 0.30 0.20 0.22 0.26 0.31 0.26 0.20 0.20 0.27 [556] 0.25 0.26 0.18 0.30 0.20 0.29 0.16 0.38 0.26 0.22 0.29 0.22 0.30 0.26 0.19 [571] 0.27 0.24 0.29 0.29 0.25 0.19 0.23 0.24 0.24 0.23 0.25 0.31 0.18 0.24 0.33 [586] 0.27 0.25 0.27 0.29 0.28 0.24 0.23 0.24 0.28 0.20 0.24 0.30 0.24 0.21 0.20 [601] 0.25 0.24 0.24 0.30 0.22 0.26 0.23 0.25 0.21 0.21 0.24 0.27 0.18 0.20 0.22 [616] 0.30 0.25 0.23 0.27 0.26 0.23 0.23 0.28 0.18 0.29 0.27 0.25 0.32 0.26 0.15 [631] 0.22 0.24 0.21 0.34 0.23 0.23 0.18 0.29 0.23 0.27 0.28 0.23 0.37 0.20 0.17 [646] 0.25 0.11 0.21 0.28 0.22 0.28 0.25 0.22 0.25 0.21 0.18 0.20 0.27 0.30 0.24 [661] 0.28 0.23 0.30 0.31 0.24 0.23 0.37 0.19 0.27 0.32 0.25 0.27 0.28 0.29 0.22 [676] 0.26 0.26 0.20 0.22 0.25 0.24 0.19 0.27 0.21 0.32 0.27 0.31 0.29 0.24 0.24 [691] 0.29 0.29 0.25 0.22 0.34 0.23 0.18 0.33 0.18 0.23 0.24 0.26 0.18 0.20 0.23 [706] 0.30 0.28 0.26 0.34 0.17 0.33 0.30 0.32 0.30 0.22 0.28 0.19 0.19 0.23 0.23 [721] 0.20 0.23 0.21 0.31 0.30 0.20 0.24 0.23 0.23 0.28 0.26 0.34 0.27 0.33 0.31 [736] 0.20 0.25 0.12 0.25 0.20 0.20 0.25 0.27 0.24 0.29 0.26 0.22 0.30 0.26 0.28 [751] 0.28 0.27 0.23 0.18 0.28 0.22 0.21 0.27 0.22 0.26 0.21 0.22 0.27 0.24 0.19 [766] 0.27 0.29 0.37 0.30 0.27 0.25 0.30 0.19 0.22 0.22 0.28 0.32 0.22 0.33 0.26 [781] 0.20 0.31 0.23 0.24 0.24 0.26 0.24 0.30 0.17 0.21 0.20 0.22 0.20 0.17 0.24 [796] 0.22 0.24 0.23 0.23 0.24 0.23 0.16 0.16 0.17 0.23 0.27 0.29 0.26 0.16 0.21 [811] 0.34 0.19 0.25 0.25 0.28 0.32 0.17 0.22 0.26 0.23 0.23 0.24 0.22 0.22 0.14 [826] 0.30 0.25 0.33 0.26 0.25 0.31 0.28 0.30 0.21 0.19 0.17 0.19 0.21 0.16 0.21 [841] 0.26 0.21 0.29 0.27 0.31 0.32 0.19 0.22 0.24 0.25 0.25 0.24 0.23 0.30 0.21 [856] 0.22 0.19 0.20 0.21 0.20 0.21 0.28 0.19 0.26 0.28 0.26 0.29 0.28 0.26 0.21 [871] 0.31 0.32 0.31 0.22 0.23 0.25 0.27 0.26 0.22 0.27 0.30 0.24 0.25 0.23 0.27 [886] 0.25 0.24 0.24 0.30 0.29 0.26 0.32 0.29 0.23 0.24 0.20 0.26 0.26 0.22 0.22 [901] 0.19 0.23 0.33 0.18 0.27 0.26 0.28 0.18 0.26 0.24 0.24 0.26 0.27 0.17 0.26 [916] 0.23 0.27 0.25 0.32 0.20 0.22 0.23 0.25 0.25 0.24 0.28 0.20 0.19 0.22 0.20 [931] 0.22 0.24 0.17 0.19 0.22 0.17 0.19 0.27 0.27 0.28 0.29 0.18 0.24 0.30 0.26 [946] 0.34 0.26 0.24 0.25 0.24 0.29 0.28 0.29 0.23 0.24 0.21 0.24 0.23 0.23 0.29 [961] 0.19 0.29 0.30 0.33 0.25 0.30 0.32 0.23 0.30 0.27 0.17 0.20 0.21 0.24 0.36 [976] 0.21 0.26 0.30 0.26 0.25 0.22 0.21 0.38 0.21 0.24 0.21 0.25 0.21 0.32 0.20 [991] 0.29 0.24 0.19 0.21 0.32 0.26 0.27 0.18 0.21 0.20 >
위의 비율의 기댓값을 (평균을) 구한다는 것이 교재가 하는 이야기
> mean.ps.k <- mean(ps.k) > mean.ps.k [1] 0.24893 >
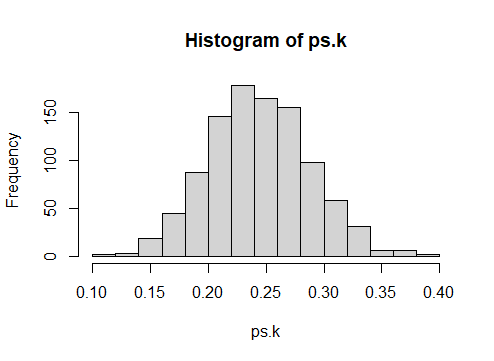
위의 결과를 histogram으로 그려보면
hist(ps.k)
이는 평균이 0.25에 (p값에) 근접하는 값이 된다. 교재의 p값이 되는 것은 k가 무한대로 큰 값을 가질 때의 이야기.
아래는 k를 1000번이 아닌 1000000번 (백만번일 때의 이야기). 평균비율이 0.25가 된다.
> set.seed(101) > k <- 1000000 > n <- 100 > p <- 1/4 > q <- 1-p > numbers.of.red.gumball <- rbinom(k, n, p) > # 아래처럼 n으로 (100개의 검볼이 총 숫자이므로) > # 나눠주면 비율을 구할 수 있다 > proportions.of.rg <- numbers.of.red.gumball/n > ps.k <- proportions.of.rg > mean.ps.k <- mean(ps.k) > mean.ps.k [1] 0.2500217 >
| references |
|---|
|
Sampling distribution of sample proportion part 1, |
|
The Sampling Distribution of the Sample Proportion |
What about variance
그렇다면 위의 분포에서의 분산값은 얼마가 될까? 그리고 표준편차값은 얼마가 될까?
\begin{eqnarray*}
\text{Variance of sample proportions} & = & Var(P_{s}) \\
& = & Var\left(\frac{X}{n}\right) \\
& = & \frac {Var(X)}{n^{2}} \\
& = & \frac {npq}{n^{2}} \\
& = & \frac {pq}{n} \\
\text{Standard deviation of sample proportions} & = & \sqrt{\frac{pq}{n}} \\
& = & \text{Standard error of sample proportions}
\end{eqnarray*}
우리는 위의 Standard deviation of sample proportions를 특별하게 standard error라고 부른다.
종합하면, Sample proportions 들에 대한 기대값과 분산은 각각 아래와 같다 (그림 참조).
$$E(P_{s}) = p \qquad\qquad\qquad Var(P_{s}) = \displaystyle \frac{pq}{n}$$
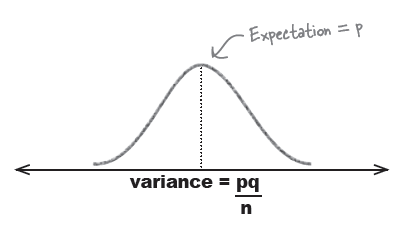
$$P_{s} \sim N\left(p,\; \frac{pq}{n}\right) $$
continuity correction: $$\pm \frac{1}{2n}$$
R에서의 simulation을 계속해서 보면
> # variance? > var.cal <- var(ps.k) > var.value <- (p*q)/n > var.cal [1] 0.001869001 > var.value [1] 0.001875 > > # standard deviation > sd.cal <- sqrt(var.cal) > sd.value <- sqrt(var.value) > sd.cal [1] 0.04323195 > sd.value [1] 0.04330127 > se <- sd.value > # 우리는 standard deviation of sample > # proportions 를 standard error라고 > # 부른다 >
위의 se는 standard deviation의 일종이므로 그 특성을 갖는다 (68, 95, 99%). 따라서 Red gumball의 비율이 1/4임을 알고 있을 때, n=100개의 gumball을 샘플링하면 (한번), red gumball의 비율은 p를 (0.25) 중심으로 위아래도 2*se 범위의 값이 나올 확률이 95%임을 안다는 것이 된다. 위에서 계산해보면;
# 위의 histogram 에서 mean 값은 이론적으로 p # standard deviation값은 se # 우리는 평균값에서 +- 2*sd.cal 구간이 95%인줄 안다. se2 <- se * 2 # 즉, 아래 구간이 lower <- p-se2 upper <- p+se2 lower upper hist(ps.k) abline(v=lower, col=2, lwd=2) abline(v=upper, col=2, lwd=2)
즉 아래의 그래프에서
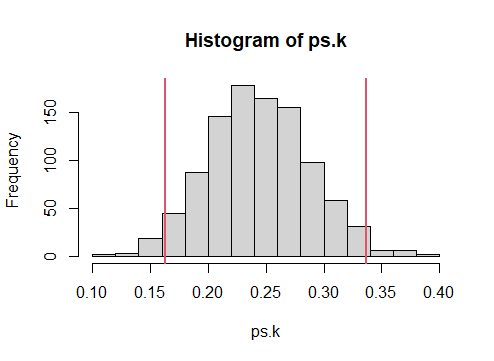
lower: 0.1633975와 (16.33975%) upper: 0.3366025 사이에서 (33.66025%) red gumaball의 비율이 나올 확률이 95%라는 이야기.
그렇다면 만약에 30% 이상이 red gumball일 확률은 무엇이라는 질문이라면
우리는 X ~ B(100, 1/4)에서 도출되는
X ~ N(p, se) 에서 P(X>_0.3)을 구하는 질문이므로
1-pnorm(0.295, p, se) 가 답이 되겠다.
1-pnorm(0.295, p, se)
[1] 0.1493488
Exercise
25% of the gumball population are red. What’s the probability that in a box of 100 gumballs, at least 40% will be red? We’ll guide you through the steps.
1. If Ps is the proportion of red gumballs in the box, how is Ps distributed?
샘플 비율에 (proportion) 대한 질문이므로, 우리는 샘플 proportion은 아래와 같은 성격을 갖는 것을 안다.
\begin{eqnarray*} P_{s} & \sim & N\left(p,\; \frac{pq}{n}\right) \\ & \sim & N\left(0.25,\; \frac{0.25*0.75}{100}\right) \\ \end{eqnarray*}
2. What’s the value of P(Ps ≥ 0.4)? Hint: Remember that you need to apply a continuity correction.
\begin{eqnarray*}
P(P_{s} \ge 0.4) & = & P(P_{s} > 0.4 - (1/(2*100)) ) \\
& = & P(P_{s} > 0.395)
\end{eqnarray*}
0.395일 때의 표준점수를 구한 후 오른 쪽 부분의 면적을 구한다.
\begin{eqnarray*}
z & = & \frac {X - \mu}{s} \\
& = & \frac {0.395 - 0.25}{\sqrt{(\frac{0.25*0.75}{100})}} \\
& = & \frac {0.145}{\sqrt{0.001875}} \\
& = & \frac {0.145}{0.04330127} \\
& = & 3.348632 \\
& \approx & 3.35
\end{eqnarray*}
위의 계산을 토대로 구해야 할 값은
\begin{eqnarray*} P(Z = z) & = & 1 - P (Z < 3.35) \\ & = & 1 - 0.9996 \\ & = & 0.0004 \end{eqnarray*}
p <- 0.25 q <- 1-p n <- 100 var <- (p*q)/(n) se <- sqrt((p*q)/(n)) o <- .4 o.c <- .4 - (1/(2*n)) o.c pnorm(o.c, p, se, lower.tail = F)
> > p <- 0.25 > q <- 1-p > n <- 100 > var <- (p*q)/(n) > se <- sqrt((p*q)/(n)) > o <- .4 > o.c <- .4 - (1/(2*n)) > o.c [1] 0.395 > pnorm(o.c, p, se, lower.tail = F) [1] 0.0004060586
Sampling distribution of sample mean
According to Mighty Gumball’s statistics for the population, the mean number of gumballs in each packet is 10, and the variance is 1. The trouble is they’ve had a complaint. One of their most faithful customers bought 30 packets of gumballs, and he found that the average number of gumballs per packet in his sample is only 8.5.
\begin{eqnarray*}
\overline{X} = \frac{X_{1} + X_{2} + . . . + X_{n}}{n}
\end{eqnarray*}
Let $ X_{1}, X_{2}, X_{3}, . . . X_{n} $ be a random sample of size of $n$.
위는 풍선검 봉지 30개로 이루어진 샘플의 평균을 이야기하고
아래는 이 평균을 계속 모았을 때의 평균을 이야기한다.
\begin{eqnarray*}
E(\overline{X}) & = & E\left(\frac{X_{1} + X_{2} + . . . + X_{n}}{n}\right) \\
& = & \frac{1}{n}\: E \left(X_{1} + X_{2} + . . . + X_{n}\right) \\
& = & \frac{1}{n}\: \left(E(X_{1}) + E(X_{2}) + . . . + E(X_{n})\right) \\
& = & \frac{1}{n}\: \left(\mu + \mu + . . . + \mu \right)\\
& = & \frac{1}{n}\: n * \mu \\
& = & \mu
\end{eqnarray*}
헷갈릴까봐 정리
| 봉지 ID | ||||||
| bag 1 | bag 2 | bag 3 | . . . . | bag n-1 | bag n | |
| 9 | 10 | 12 | . . . . | 8 | 7 | |
| 5 | 12 | 9 | . . . . | 12 | 10 | |
| 11 | 8 | 10 | . . . . | 10 | 9 | |
| . . . | .. | .. | .. | . . . . | .. | .. |
| mean of $\overline{X}s = E(\overline{X})$ | mean of bag 1 $ X_{1} = 10 $ | mean of bag 2 $ X_{2} = 10 $ | mean of bag 3 $ X_{3} = 10 $ | . . . . | mean of bag n-1 $ X_{n-1} = 10 $ | mean of bag n $ X_{n} = 10 $ |
Variance of sample means
Statistics Magnets
\begin{eqnarray*} \overline{X} = \frac{X_{1} + X_{2} + . . . + X_{n}}{n} \end{eqnarray*}
\begin{align*} Var(\overline{X}) & = Var \left(\frac{X_{1} + X_{2} + . . . + X_{n}}{n}\right) \\ & = \frac {1}{n^2} Var \left(X_{1} + X_{2} + . . . + X_{n} \right) \\ & = \frac{1}{n^2} (\sigma^2 + \sigma^2 + . . . + \sigma^2) \\ & = \frac{1}{n^2} n * (\sigma^2) \\ & = \frac{\sigma^2}{n} \end{align*}
\begin{eqnarray} E(\overline{X}) & = & \mu_{\overline{X}} \; = \; \mu \\ Var(\overline{X}) & = & \sigma^{2}_{\overline{X}} \; = \; \frac{\sigma^2}{n} \\ SD(\overline{X}) & = & \sigma_{\overline{X}} \; = \; \frac{\sigma}{\sqrt{n}} \end{eqnarray}
\begin{eqnarray*} \text{standard error} & = & \text{standard deviation of sample means} \\ & = & \frac{\sigma}{\sqrt{n}} \\ & = & \sqrt{\frac{\sigma^{2}}{n}} \end{eqnarray*}
\begin{eqnarray*} \text{If} \; X \sim N(\mu, \ \sigma^2), \;\; \text{then} \; \overline{X} \sim N(\mu, \ \frac{\sigma^2}{n}) \end{eqnarray*}
| reference |
|---|
|
sampling distribution of x bar (sample mean) |
|
deriving mean and variance of (sampling distribution of) sample mean |
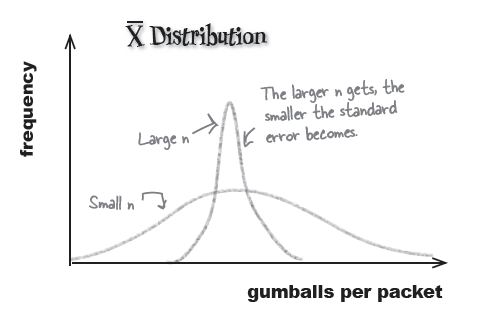
Distribution of sample means: CLT
Though X may NOT be normally distributed, $\overline{X}$ is, if n is large enough.
CLT, see Central Limit Theorem
Using CLT for the binomial distribution
$X \sim B(n, p)$ 에서 $\mu = np$, $\sigma^2 = npq$ 이고,
n이 30이 넘는 조건에서 이항분포가 정상분포를 이룬다고 하므로
$\overline{X} \sim N(\mu, \frac{\sigma^2}{n})$에 대입해 보면:
$$\overline{X} \sim N(np, \; pq) $$
for the Poisson distribution
$X \sim Po(\lambda)$, n이 30이 넘는 조건에서, $\mu = \sigma^2 = \lambda$ 이다. 이를 $\overline{X} \sim N(\mu, \frac{\sigma^2}{n})$에 대입해 보면:
$$\overline{X} \sim N(\lambda, \; \frac{\lambda}{n}) $$
Exercise
Let’s apply this to Mighty Gumball’s problem.
- The mean number of gumballs per packet is 10, and the variance is 1.
- If you take a sample of 30 packets,
- what’s the probability that the sample mean is 8.5 gumballs per packet or fewer?
We’ll guide you through the steps.
$\overline{X}$?
$\overline{X} \sim N(\mu, \frac{\sigma^2}{n})$ 이고, n = 30 일 경우는
$$\overline{X} \sim N(10, \frac{1}{30})$$
$P (\overline{X} < 8.5)$ 을 묻는 문제이므로
\begin{eqnarray*}
z & = & \frac{8.5-10}{\sqrt{\frac{1}{30}}} \\
& = & -8.22
\end{eqnarray*}
따라서, 위의 문제는 $P(Z < z) = P(Z < -8.22)$를 묻는 문제
> pnorm(-8.22) [1] 1.017516e-16 > pnorm(8.5, 10, sqrt(1/30)) # or . . . . [1] 1.053435e-16 >
discrepancy?
> a <- sqrt(1/30) > b <- 8.5-10 > b/a [1] -8.215838 > pnorm(b/a) [1] 1.053435e-16
Recap
Distribution of Sample Proportions, $Ps$,
when sampling n entities (repeatedly) from a population whose proportion is p.
\begin{eqnarray*}
Ps & \sim & N(p, \frac{pq}{n}) \\
\end{eqnarray*}
Distribution of Sample Means, $\overline{X}$
when sampling a sample whose size is n from a population whose mean is $\mu$ and variance is $\sigma^2$.
\begin{eqnarray*}
\overline{X} & \sim & N(\mu, \frac{\sigma^2}{n}) \\
\end{eqnarray*}