This is an old revision of the document!
Table of Contents
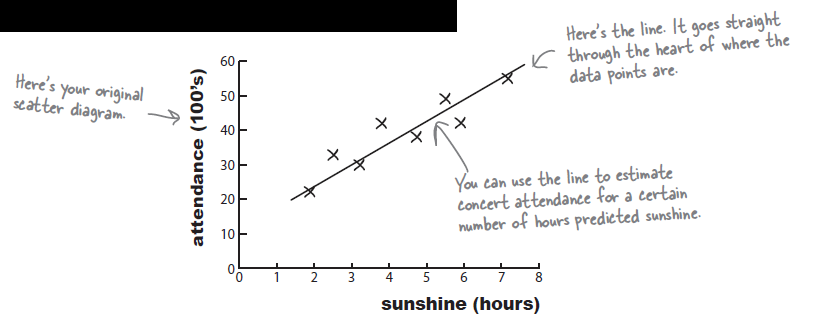
Correlation and Regression: What's My Line?
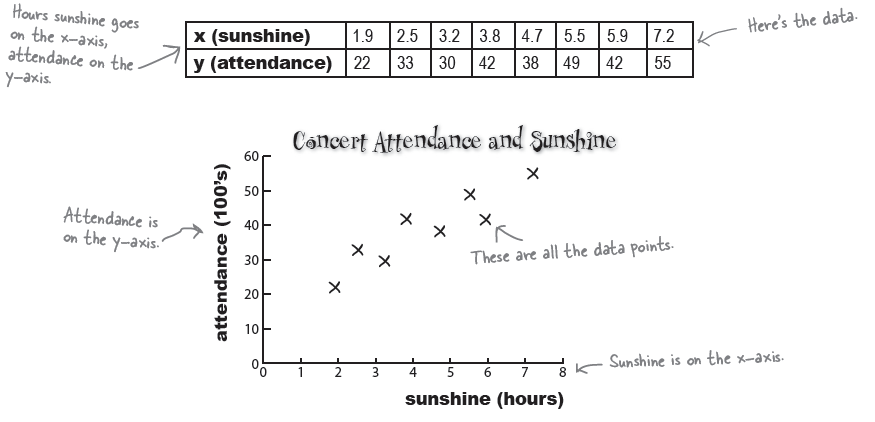
> s <- c(1.9,2.5,3.2,3.8,4.7,5.5, 5.9, 7.2)
> c <- c(22,33,30,42,38,49,42,55)
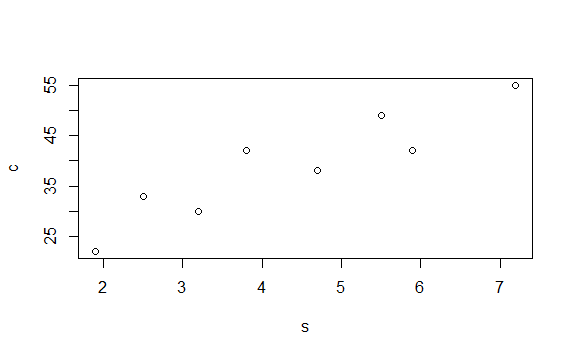
> plot(s,c)
> df <- data.frame(s,c)
> df
s c
1 1.9 22
2 2.5 33
3 3.2 30
4 3.8 42
5 4.7 38
6 5.5 49
7 5.9 42
8 7.2 55
> plot(df)
Predict values with a line of best fit
\begin{eqnarray*} b & = & \frac{\Sigma{(x-\overline(x))(y-\overline(y))}}{\Sigma{(x-\overline{x})^2}} \\ & = & \frac{\text{SP}}{\text{SS}_{x}} \\ a & = & \overline{y} - b \overline{x} \end{eqnarray*}
> mod <- lm(c~s, data=df)
> summary(mod)
Call:
lm(formula = c ~ s, data = df)
Residuals:
Min 1Q Median 3Q Max
-5.2131 -3.0740 -0.9777 3.9237 5.9933
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 15.7283 4.4372 3.545 0.01215 *
s 5.3364 0.9527 5.601 0.00138 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 4.571 on 6 degrees of freedom
Multiple R-squared: 0.8395, Adjusted R-squared: 0.8127
F-statistic: 31.37 on 1 and 6 DF, p-value: 0.001379
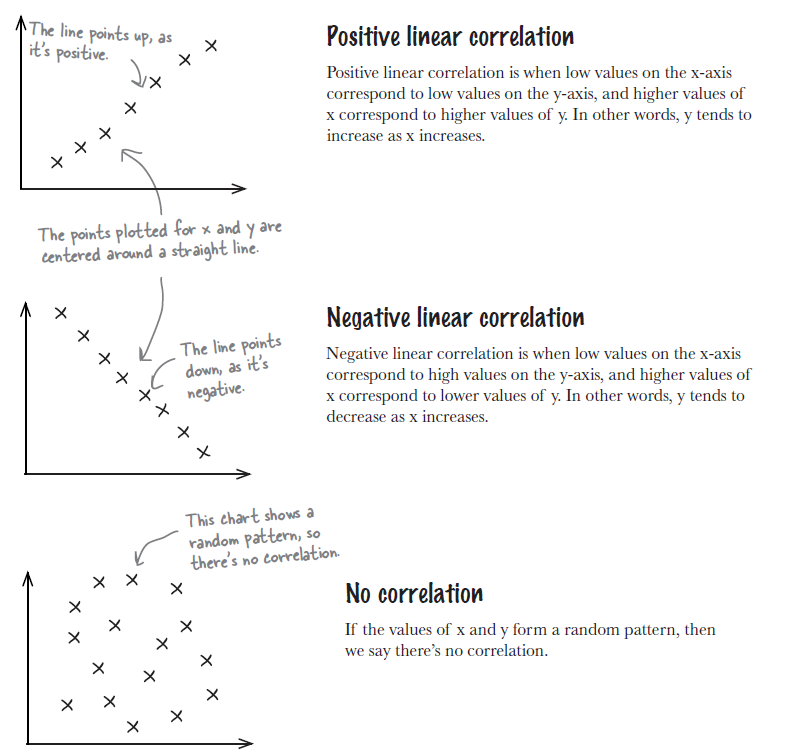
Correlation
Textbook says:
\begin{align} r = & b * \frac {sd(x)}{sd(y)} \\ = & b * \sqrt{\frac {SS_X} {SS_Y}} \;\;\; \because \left(b = \frac {SP}{SS_X} \right) \nonumber \\ = & \frac {SP}{SS_X} * \frac {\sqrt{SS_X}} {\sqrt{SS_Y}} \nonumber \\ = & \frac {SP}{\sqrt{SS_X * SS_Y}} \nonumber \\ = & \frac {COV}{SD(X) SD(Y)} \end{align}
Regression page says:
\begin{eqnarray}
R^2 & = & \frac{\text{SS}_{reg}}{\text{SS}_{total}} \\
& = & \frac{ \text{SS}_{total} - \text{SS}_{res}} {\text{SS}_{total}} \nonumber \\
& = & 1 - \frac{\text{SS}_{res}} {\text{SS}_{total}} \\
\end{eqnarray}
\begin{eqnarray*} & \text{Note that (1), (2) are the same.} \nonumber \\ & \text{Therefore,} \nonumber \\ & r = \sqrt{R^2} \\ \end{eqnarray*}
We, from correlation wiki page, also addressed that r (correlation coefficient value) can be obtained through
\begin{eqnarray*}
r & = & \frac {Cov(x,y)} {sd(x)*sd(y)} \\
\end{eqnarray*}
see pearson_s_r
아래는 위의 세 가지 방법으로 R에서 r 값을 구해본 것이다.
# check the coefficient from the lm analysis b <- summary(mod)$coefficients[2,1] b df sd.x <- sd(df$s) sd.y <- sd(df$c) # 첫 번째 r.value1 <- b * (sd.x/sd.y) r.value1 # 두 번째 # rsquared r.value2 <- sqrt(summary(mod)$r.squared) r.value2 # or cov.sc <- cov(df$s, df$c) r.value3 <- cov.sc/(sd.x*sd.y) r.value3
아래는 위의 아웃풋
> # check the coefficient from the lm analysis
> b <- summary(mod)$coefficients[2,1]
> b
[1] 5.336411
> df
s c
1 1.9 22
2 2.5 33
3 3.2 30
4 3.8 42
5 4.7 38
6 5.5 49
7 5.9 42
8 7.2 55
> sd.x <- sd(df$s)
> sd.y <- sd(df$c)
>
> # 첫 번째
> r.value1 <- b * (sd.x/sd.y)
> r.value1
[1] 0.9162191
>
> # 두 번째
> # rsquared
> r.value2 <- sqrt(summary(mod)$r.squared)
> r.value2
[1] 0.9162191
>
> # or
> cov.sc <- cov(df$s, df$c)
> r.value3 <- cov.sc/(sd.x*sd.y)
>
> r.value3
[1] 0.9162191
>
exercise
re <- c(4, 4.5, 5, 5.5, 6, 6.5, 7) we <- c(12, 10, 8, 9.5, 8, 9, 6) mean.re <- mean(re) mean.we <- mean(we) sd.re <- sd(re) sd.we <- sd(we) var.re <- var(re) var.we <- var(we) ss.re <- sum((re-mean.re)^2) ss.we <- sum((we-mean.we)^2) sp <- sum((re-mean.re)*(we-mean.we)) df <- 7-1 cov.rewe <- sp/df cov.rewe2 <- cov(re,we) mean.re mean.we sd.re sd.we var.re var.we ss.re ss.we sp df cov.rewe cov.rewe2 # r, b, r square r.val <- sp / (sqrt(ss.re*ss.we)) r.val b <- sp / ss.re b a <- mean.we - (b * mean.re) a r.sq <- r.val^2 r.sq cor(re,we) m1 <- lm(we~re) summary(m1)
######################## ss <- c(1.9, 2.5, 3.2, 3.8, 4.7, 5.5, 5.9, 7.2) at <- c(22, 33, 30, 42, 38, 49, 42, 55) mean.ss <- mean(ss) mean.at <- mean(at) ss.ss <- sum((ss-mean.sa)^2) ss.at <- sum((at-mean.at)^2) df <- 8-1 var.ss <- ss.ss/df var.at <- ss.at/df sd.ss <- sqrt(var.ss) sd.at <- sqrt(var.at) sp.ssat <- sum((ss-mean.ss)*(at-mean.at)) cov.ssat <- sp.ssat/df