> rm(list=ls())
> rnorm2 <- function(n,mean,sd){ 
+   mean+sd*scale(rnorm(n)) 
+ }
> 
> ss <- function(x) {
+   sum((x-mean(x))^2)
+ }
> 

….
필요한 펑션

• rnorm2는 평균과 표준편차값을 (mean, sd) 갖는 n 개의 샘플을 랜덤하게 추출하는 것
• ss는 sum of square 값을 구하는 펑션
• ss는 ss/n-1 의 variance 혹은 mean square값을 구할 때의 분자부분으로
• error 혹은 residual의 제곱의 합이라고 부를 수 있다 (variance 참조)

> ################################
> N.p <- 1000000
> m.p <- 100
> sd.p <- 10
> 
> p1 <- rnorm2(N.p, m.p, sd.p)
> mean(p1)
[1] 100
> sd(p1)
[1] 10
> 
> p2 <- rnorm2(N.p, m.p+20, sd.p)
> mean(p2)
[1] 120
> sd(p2)
[1] 10
> 
> m.p1 <- mean(p1)
> sd.p1 <- sd(p1)
> var(p1)
     [,1]
[1,]  100
> 

• rnorm2 펑션을 이용하여 p1과 p2 모집단을 구한다.
• 각 모집단의 평균은 100과 120이고, 표준편차는 모두 10이다.
• 모집단의 크기는 각각 백만이다.

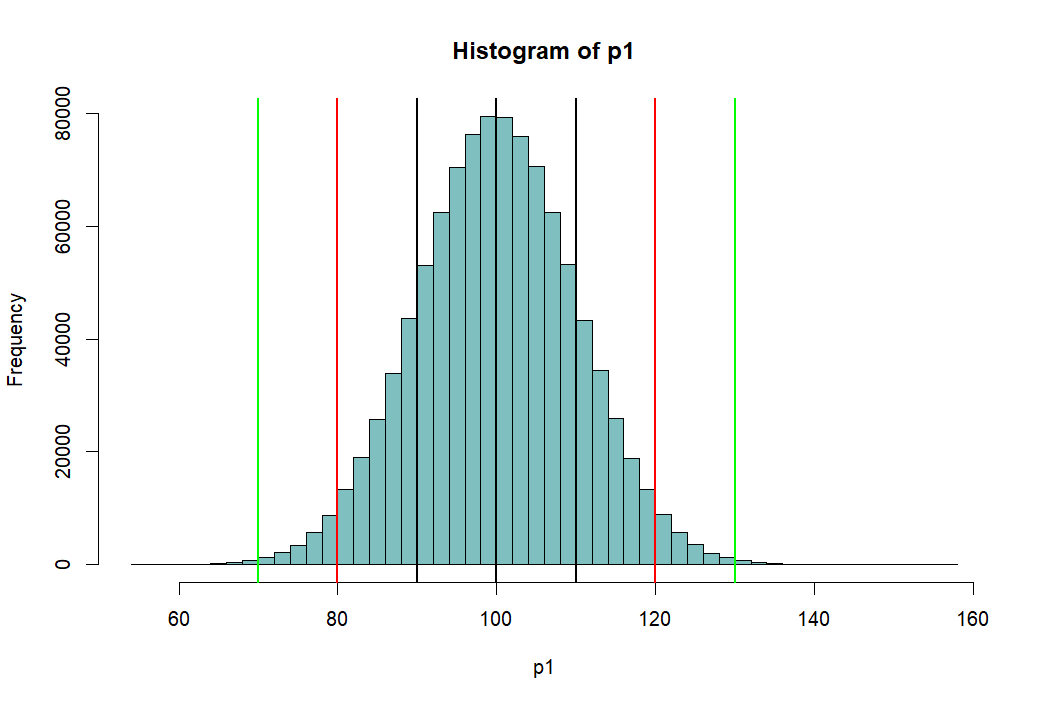
> hist(p1, breaks=100, col=rgb(1,1,1,1))
> abline(v=mean(p1),lwd=2)
> abline(v=mean(p1)-sd(p1), lwd=2)
> abline(v=mean(p1)+sd(p1), lwd=2)
> abline(v=c(m.p1-2*sd.p1, m.p1+2*sd.p1), lwd=2, col='red')
> abline(v=c(m.p1-3*sd.p1, m.p1+3*sd.p1), lwd=2, col='green')
> 
> # area bet black = 68%
> # between red = 95%
> # between green = 99%
> 
> pnorm(m.p1+sd.p1, m.p1, sd.p1)
[1] 0.8413447
> pnorm(m.p1-sd.p1, m.p1, sd.p1)
[1] 0.1586553
> pnorm(m.p1+sd.p1, m.p1, sd.p1) - 
+   pnorm(m.p1-sd.p1, m.p1, sd.p1)
[1] 0.6826895
> 
> pnorm(m.p1+2*sd.p1, m.p1, sd.p1) - 
+   pnorm(m.p1-2*sd.p1, m.p1, sd.p1)
[1] 0.9544997
> 
> pnorm(m.p1+3*sd.p1, m.p1, sd.p1) - 
+   pnorm(m.p1-3*sd.p1, m.p1, sd.p1)
[1] 0.9973002
> 
> m.p1
[1] 100
> sd.p1
[1] 10
> 
> (m.p1-m.p1)/sd.p1
[1] 0
> ((m.p1-sd.p1) - m.p1) / sd.p1
[1] -1
> (120-100)/10 
[1] 2
> pnorm(1)-pnorm(-1)
[1] 0.6826895
> pnorm(2)-pnorm(-2)
[1] 0.9544997
> pnorm(3)-pnorm(-3)
[1] 0.9973002
> 
> 1-pnorm(-2)*2
[1] 0.9544997
> pnorm(2)-pnorm(-2)
[1] 0.9544997
> 
> pnorm(120, 100, 10)
[1] 0.9772499
> pnorm(2)-pnorm(-2)
[1] 0.9544997
> 
>
>
>
> 
>
>
>

….
pnorm 펑션

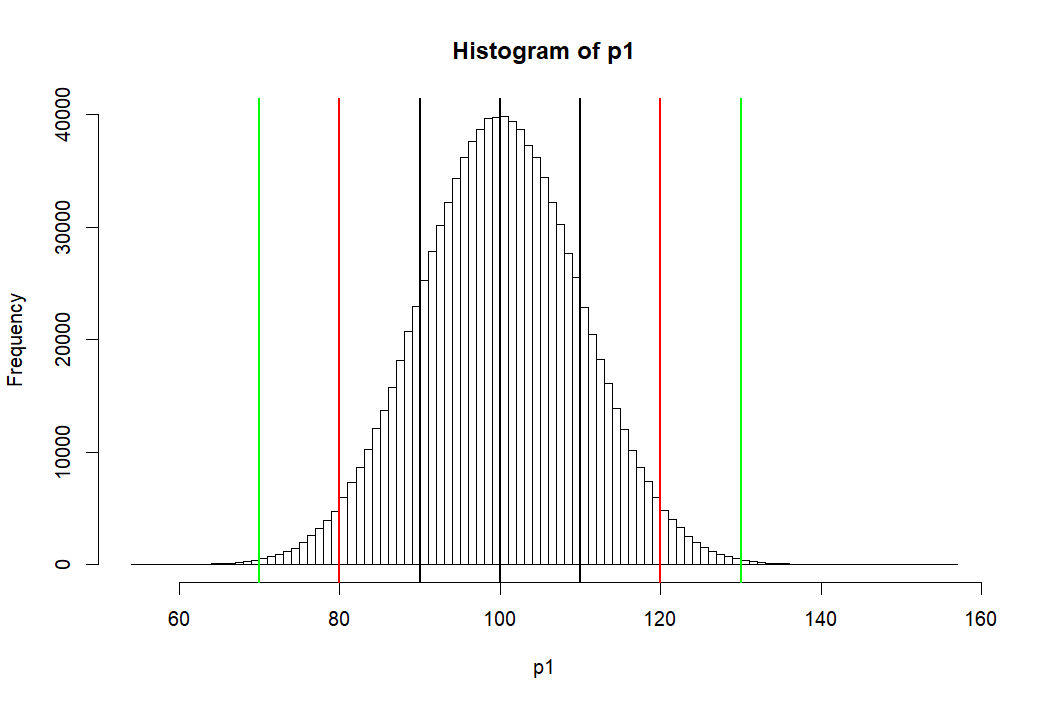
• 위의 histogram에서 검정색의 선은 p1의 standard deviation값인 10씩 좌우로 그린것 (90과 110)
• 붉은 색선은 80, 120
• 녹색선은 70, 130 선을 말한다
• 고등학교 때, Normal distribution (정상분포의) 경우
• 평균을 중심으로 위아래로 SD값 하나씩 간 간격의 probability는 (면적은) 68%
• 두 개씩 간 값은 95%
• 세 개씩 간 값은 99% 라고 배웠다.
• pnorm은 percentage를 구하는 R의 명령어

• pnorm(m.p1+sd.p1, m.p1, sd.p1) 은
  • 정규분포곡선에서
  • 평균값과 표준편차값을 더한 값 (100+10=110) 을 기준으로
  • 왼쪽의 부분이 몇 퍼센트인가를 구해주는 명령어
  • m.p1+sd.p1은 110이므로
  • 오른 쪽 검정색을 기준으로 왼쪽의 퍼센티지를 묻는 것
  • 답은 0.8413447
  • pnorm(m.p1-sd.p1, m.p1, sd.p1) - pnorm(90, 100, 10)이므로
  • 왼쪽 검정색 선을 기준으로 왼쪽의 퍼센티지를 묻는 것
  • 답은 0.1586553
  • 전자에서 후자를 빼 준 값은 두개의 검정색 선의 안쪽 면적으로 묻는 것
  • 답은 0.6826895
• 이 0.6826895 이 우리가 배운 68%
• 그렇다면 두 개씩 간 면적은 (붉은 색 선의 안쪽 부분)
  • pnorm(m.p1+2*sd.p1, m.p1, sd.p1) - pnorm(m.p1-2*sd.p1, m.p1, sd.p1) = 0.9544997
  • 0.9544997 혹은 95.44997%
  • 이것이 우리가 배운 95%
• 마찬가지로 녹색선 가운데 부분은 pnorm(m.p1+3*sd.p1, m.p1, sd.p1) - pnorm(m.p1-3*sd.p1, m.p1, sd.p1) 로 구할 수 있는데 답은
• 0.9973002

• pnorm명령어는 pnorm(score, mean, sd)와 같이 사용하여 퍼센티지값을 구할 수 있는데
• pnorm(score)만으로 구하면, mean과 sd가 각각 0, 1을 default값으로 하고 생략이 된 것
• 위의 p1 모집단도 두번째 방법으로 구해 볼 수 있는데, 그렇게 하기 위해서
• p1을 표준점수화 하면 됨
• 표준점수화 한다는 뜻은 p1집합의 평균과 표준편차 값을 0과 1로 만든다는 것
• p1 모든 원소를 표준점수화하는 것은 각 점수와 평균점수 간의 차이에 sd가 몇개나 들어가는 지 구하는 것. 즉,
  • $ \dfrac {(\text{score} - \text{m.p1})} {\text{sd.p1}} $
  • 100점은 표준점수로 0이 된다 $ (100-100) / 10 = 0 $
  • 110점은 1
  • 90점은 -1
  • 115점은 1.5
  • 130점은 30/10 = 3 점으로 계산될 수 있다.
• 그렇다면 위의 pnorm(m.p1+sd.p1, m.p1, sd.p1)은 pnorm(1)과 같은 것
• pnorm(110, 100, 10) 이고 이 때 110점은 표준점수로 1 이다.
• 따라서 위의 68%, 95%, 99%는 pnorm(1)-pnorm(-1)과 같이 구할 수 있다.

> zscore <- (120-100)/10
> pnorm(zscore)-pnorm(-zscore)
[1] 0.9544997
> zscore
[1] 2
> 
> 
> pnorm(-1)
[1] 0.1586553
> pnorm(1, 0, 1, lower.tail = F)
[1] 0.1586553
> pnorm(110, 100, 10, lower.tail = F)
[1] 0.1586553
> zscore <- (110-100)/10
> pnorm(zscore, lower.tail = F)
[1] 0.1586553
> 
> pnorm(118, 100, 10, lower.tail = F)
[1] 0.03593032
> pnorm(18/10, lower.tail = F)
[1] 0.03593032
> 

….

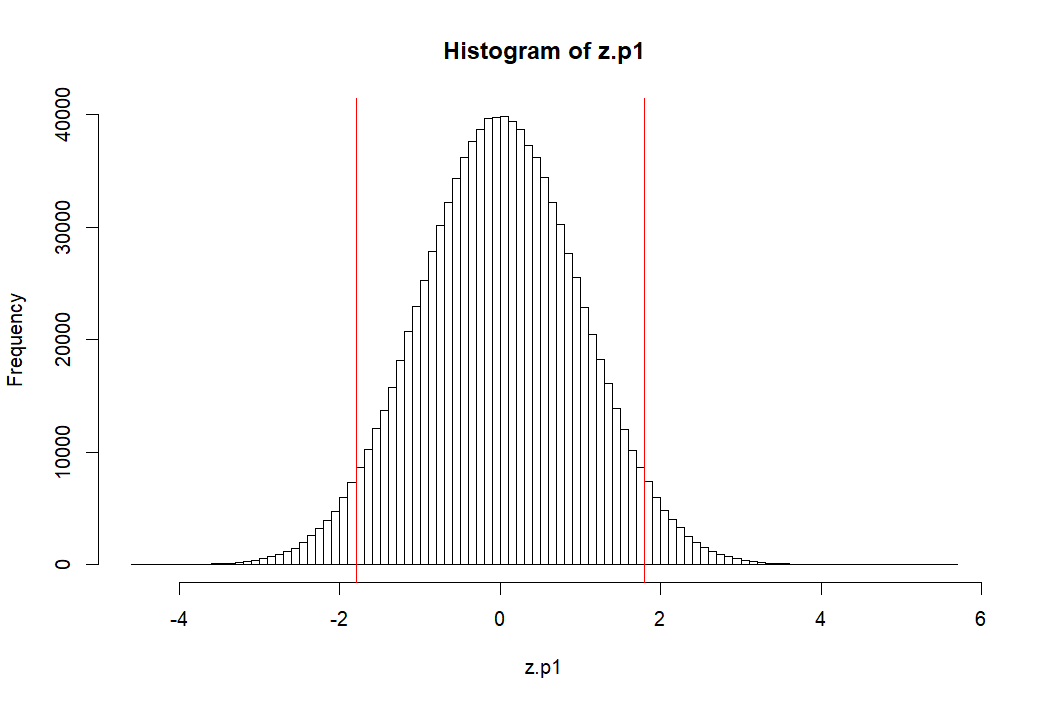
> z.p1 <- (p1-mean(p1))/sd(p1)
> mean(z.p1)
[1] -2.319195e-17
> round(mean(z.p1),10)
[1] 0
> sd(z.p1)
[1] 1
> pnorm(1.8)-pnorm(-1.8)
[1] 0.9281394
> 
> hist(z.p1, breaks=100, col=rgb(0,0,0,0))
> abline(v=c(m.p1, -1.8, 1.8), col='red')
> 1-(pnorm(1.8)-pnorm(-1.8))
[1] 0.07186064
> 
> 

….
p1 모집단의 모든 원소를 표준점수화 하기

• z.p1 ← (p1-mean(p1))/sd(p1)
• 평균과 표준편차는 각각 0, 1이 된다 (mean(z.p1), sd(z.p1))
• 그렇다면 이 표준점수화한 분포에서 -1.8과 1.8 사이를 제외한 바깥 쪽 부분의 면적은 (probability는)
• 1-(p(1.8)-p(-1.8))과 같이 구할 수 있다.
• 답은 약 7% 정도

> pnorm(1)-pnorm(-1)
[1] 0.6826895
> 1-(pnorm(-1)*2)
[1] 0.6826895
> 
> pnorm(2)-pnorm(-2)
[1] 0.9544997
> 1-(pnorm(-2)*2)
[1] 0.9544997
> 
> 1-(pnorm(-3)*2)
[1] 0.9973002
> 

….

> #
> hist(p1, breaks=100, col=rgb(1,1,1,1))
> abline(v=mean(p1),lwd=2)
> abline(v=mean(p1)-sd(p1), lwd=2)
> abline(v=mean(p1)+sd(p1), lwd=2)
> abline(v=c(m.p1-2*sd.p1, m.p1+2*sd.p1), lwd=2, col='red')
> abline(v=c(m.p1-3*sd.p1, m.p1+3*sd.p1), lwd=2, col='green')
> 
> # 68%
> a <- qnorm(.32/2)
> b <- qnorm(1-.32/2)
> c(a, b)
[1] -0.9944579  0.9944579
> c(-1, 1)
[1] -1  1
> 
> # 95%
> c <- qnorm(.05/2)
> d <- qnorm(1-.05/2)
> c(c, d)
[1] -1.959964  1.959964
> c(-2,2)
[1] -2  2
> # 99% 
> e <- qnorm(.01/2)
> f <- qnorm(1-.01/2)
> c(e,f)
[1] -2.575829  2.575829
> c(-3,3)
[1] -3  3
> 
> pnorm(b)-pnorm(a)
[1] 0.68
> c(a, b)
[1] -0.9944579  0.9944579
> pnorm(d)-pnorm(c)
[1] 0.95
> c(c, d)
[1] -1.959964  1.959964
> pnorm(f)-pnorm(e)
[1] 0.99
> c(e, f)
[1] -2.575829  2.575829
> 
> qnorm(.5)
[1] 0
> qnorm(1)
[1] Inf
> 
> 

qnorm

• qnorm는 pnorm의 반대값을 구하는 명령어
• 히스토그램에서 검정 색 부분의 바깥 쪽 부분은 32%이고 왼 쪽의 것은 이것의 반인 16% 이다.
• 이 16% 에 해당하는 표준점수가 무엇인가를 묻는 질문이 qnorm(.32/2) 혹은 qnorm(.32/2, 0, 1)
• 원점수일 경우에 대입해서 물어본다면 qnorm(.32/2, 100, 10)과 같이 하면 된다 (혹은 qnorm(.32/2, m.p1, sd.p1) ).
• 위의 명령어에 대한 답은 우리가 가장 쉽게 이해한 방법에 의하면
• -1 혹은 90 이렇게 될 것이다.
• 하지만 위에서 봤던 것처럼 pnorm(1)-pnorm(-1)이 정확히
• 0.6826895 인 것처럼, 우리가 이해한 방법은 정확한 값을 구해주지는 않는다.
• 마찬가지로 qnorm(0.05/2)와 qnorm(1-(0.05/2))는
• 표준편차 값인 1이 왼쪽으로 두개 내려가고 오른 쪽으로 두개 올라간 값의 quotient값을 구하는 것이므로
• 즉, 위의 histogram에서 붉은 색 부분의 바깥 쪽 면적에 해당하는 점수를 물어보는 것이므로
• -2와 2라고 대답해도 되지만 정확한 답은 아래와 같다 (1.96).

> qnorm(0.05/2)
[1] -1.959964
> qnorm(1-(0.05/2))
[1] 1.959964
> 

• 이에 해당하는 원점수 (p1 원소에 해당하는) 값은 80과 120이 아니라 아래와 같을 것이다.

> qnorm(0.05/2, 100, 10)
[1] 80.40036
> qnorm(1-(0.05/2), 100, 10)
[1] 119.5996
> 

> ################################
> hist(p1, breaks=50, col = rgb(1, 0, 0, 0.5),
+      main = "histogram of p1 and p2",)
> abline(v=mean(p1), col="black", lwd=3)
> hist(p2, add=T, breaks=50, col=rgb(0,0,1,.5))
> abline(v=mean(p2), col="violet", lwd=3)
> 

> s.size <- 10
> 
> means.temp <- c()
> s1 <- sample(p1, s.size, replace = T)
> mean(s1)
[1] 99.64273
> means.temp <- append(means.temp, mean(s1))
> means.temp <- append(means.temp, mean(sample(p1, s.size, replace = T)))
> means.temp <- append(means.temp, mean(sample(p1, s.size, replace = T)))
> means.temp <- append(means.temp, mean(sample(p1, s.size, replace = T)))
> means.temp <- append(means.temp, mean(sample(p1, s.size, replace = T)))
> means.temp
[1]  99.64273 107.15516 103.81192 103.12311 105.88372
> 

….

• s.size는 10으로 우선 고정하고
• 한 샘플을 취하여 그 평균값을 means.temp 메모리에 add한다 (저장하는 것이 아니라 means.temp에 붙힌다).
• 그 다음 샘플의 평균을 다시 means.temp에 저장한다
• 그 다음 . . . 모두 5번을 하고 출력을 해본다

> iter <- 1000000
> # means <- c()
> means <- rep(NA, iter)
> for (i in 1:iter) {
+   # means <- append(means, mean(sample(p1, s.size, replace = T)))
+   means[i] <- mean(sample(p1, s.size, replace = T))
+ }
> length(means)
[1] 1000000
> mean(means)
[1] 99.99544
> sd(means)
[1] 3.161886
> se.s <- sd(means)
> 
> hist(means, breaks=100, col=rgb(.1, 0, 0, .5))
> abline(v=mean(means), col="red", lwd=2)
> 

….

> # now we want to get sd of this distribution
> lo1 <- mean(means)-se.s
> hi1 <- mean(means)+se.s
> lo2 <- mean(means)-2*se.s
> hi2 <- mean(means)+2*se.s
> lo3 <- mean(means)-3*se.s
> hi3 <- mean(means)+3*se.s
> 
> hist(means, 
+      xlim = c(mean(means)-5*sd(means), mean(means)+10*sd(means)), 
+      col = rgb(1, 0, 0, .5))
> abline(v=mean(means), col="black", lwd=2)
> # abline(v=mean(p2), colo='darkgreen', lwd=3)
> abline(v=c(lo1, hi1, lo2, hi2, lo3, hi3), 
+        col=c("green","green", "blue", "blue", "orange", "orange"), 
+        lwd=2)
> 

….

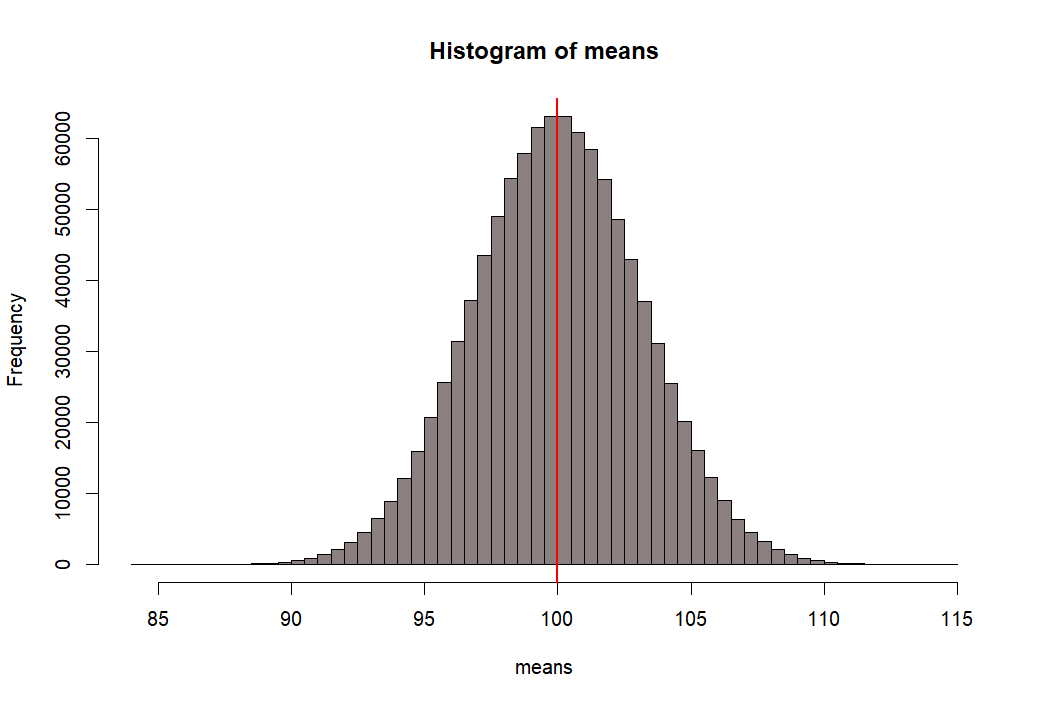
• 위 백만개의 샘플평균이 모인 집합의 히스토그램을 그리고
• 그 집합의 표준편차값을 수직선으로 표시하기 위해서
• mean(means) +- se.s 와 같은 방법을 쓴 후 그래프로 그린다.
• 아래에서 선 하나씩의 길이는 means 집합의 (distribution of sample means)
• 표준편차값이다.
• 이 표준편차 값을 위에서 sd(means)로 구한 후에 se.s로 저장한 적이 있다.
• 그리고 그 값은 3.161886 이었다.

> se.s
[1] 3.161886

> # meanwhile . . . .
> se.s
[1] 3.161886
> 
> se.z <- sqrt(var(p1)/s.size)
> se.z <- c(se.z)
> se.z
[1] 3.162278
> 
> # sd of sample means (sd(means))
> # = se.s
> 
> # when iter value goes to 
> # unlimited value:
> # mean(means) = mean(p1) 
> # and
> # sd(means) = sd(p1) / sqrt(s.size)
> # that is, sd(means) = se.z
> # This is called CLT (Central Limit Theorem)
> mean(means)
[1] 99.99544
> mean(p1)
[1] 100
> sd(means)
[1] 3.161886
> var(p1) 
     [,1]
[1,]  100
> sqrt(var(p1)/s.size)
         [,1]
[1,] 3.162278
> se.z
[1] 3.162278
> 
> sd(means)
[1] 3.161886
> se.s 
[1] 3.161886
> se.z
[1] 3.162278
> 
> # because CLT
> loz1 <- mean(p1)-se.z
> hiz1 <- mean(p1)+se.z
> loz2 <- mean(p1)-2*se.z
> hiz2 <- mean(p1)+2*se.z
> loz3 <- mean(p1)-3*se.z
> hiz3 <- mean(p1)+3*se.z
> 
> c(lo1, loz1)
[1] 96.83356 96.83772
> c(lo2, loz2)
[1] 93.67167 93.67544
> c(lo3, loz3)
[1] 90.50978 90.51317
> 
> c(hi1, hiz1)
[1] 103.1573 103.1623
> c(hi2, hiz2)
[1] 106.3192 106.3246
> c(hi3, hiz3)
[1] 109.4811 109.4868
> 
> 

….

• 그런데 이 값은 (se.s = 3.161886)
• se.z 를 구하는 방법과 거의 같은 값을 갖는다 3.162278

> se.z <- sqrt(var(p1)/s.size)
> se.z <- c(se.z)
> se.z
[1] 3.162278

• 사실, 우리가 백만 번의 샘플을 취해서 구한 means 집합의 평균과 표준편차 값은
  • 이것을 정확하게는 mean of the distribution of sample means,
  • standard deviation of the distribution of sample means 라고 부른다
  • 그리고 standard deviation of the distribution of sample means를 흔히
  • standard error라고 부른다.
  • script에서 se.s 그리고 se.z 와 같은 se를 쓴 이유도 standard error 값을 구한 것이기 때문이다.
• 만약에 백만 번이 아니라 무한 대로 더 큰 숫자를 사용한다고 하면
• 위의 se.z 값을 구하는 식의 값을 갖게 된다. 이것을 말로 풀어서 설명하면
• 샘플평균들의 집합에서 표준편차 값은
• 원래 모집단의 분산값을 샘플사이즈로 나누어준 값에 제곱근을 씌워서 구할 수 있다이다 (아래 Latex 정리에서 3번)

\begin{eqnarray*} \overline{X} \sim \displaystyle \text{N} \left(\mu, \dfrac{\sigma^{2}}{n} \right) \end{eqnarray*}

\begin{eqnarray} & & \text{Normal distribution of sample means.} \\ & & \mu_{\overline{X}} = \mu \\ & & (\sigma_{\overline{X}})^2 = \frac{\sigma^2}{n} \;\; \text{or} \;\; \sigma_{\overline{X}} = \frac{\sigma}{\sqrt{n}} \end{eqnarray}

see Central Limit Theorem and Sampling Distribution

• 즉, 샘플평균을 모은 집합의 분산값은 그 샘플이 추출된 원래 population의 분산값을 샘플크기로 (sample size) 나누어 준 값이다.
• 즉, var(means) = var(p1) / s.size
• 따라서, std(means) = sqrt(var(p1) / s.size)
• 더하여 그 샘플평균 집합의 평균 값은 population의 평균값이 된다
• 즉, mean(means) = mean(p1)

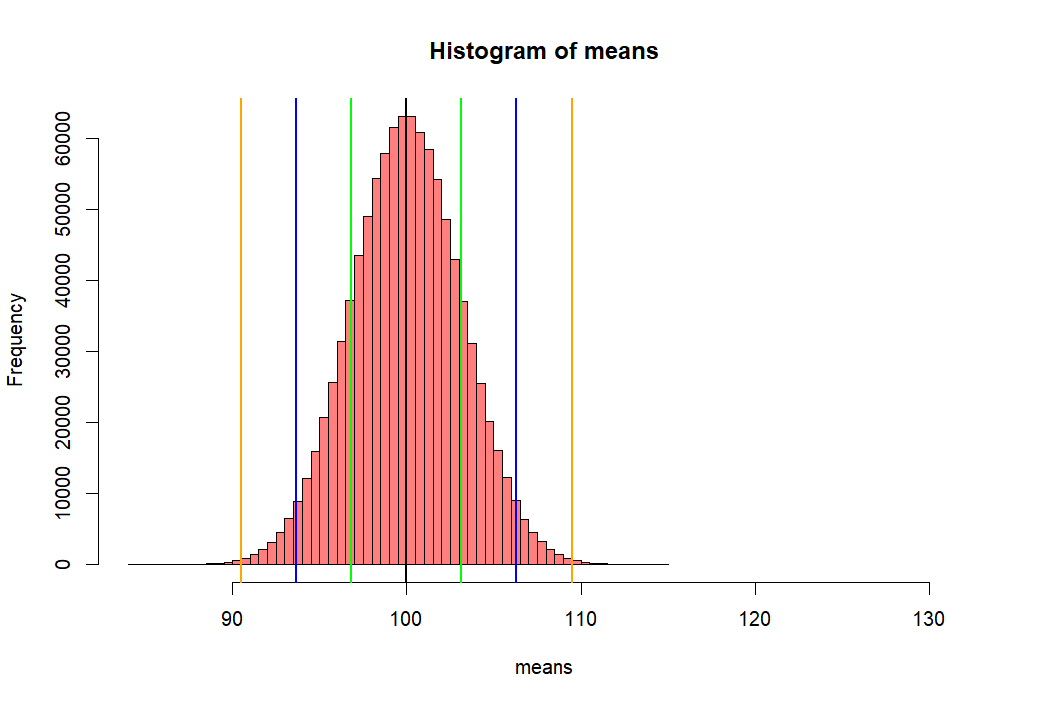
• 따라서 lo, hi에 해당하는 means분포의 값을 mean(means) +- sd(means)로 구했었는데,
• 샘플평균의 분포를 무한대 번을 했다고 하면 사실 이 값은
• mean(p1) +- se.z 로 구하는 것이 정확할 것이다.
• 여기서 se.z = sqrt(var(p1)/s.size))
• loz1 - hiz1, loz2 - hiz2 값들은 이렇게 구한 값들이다.

참고

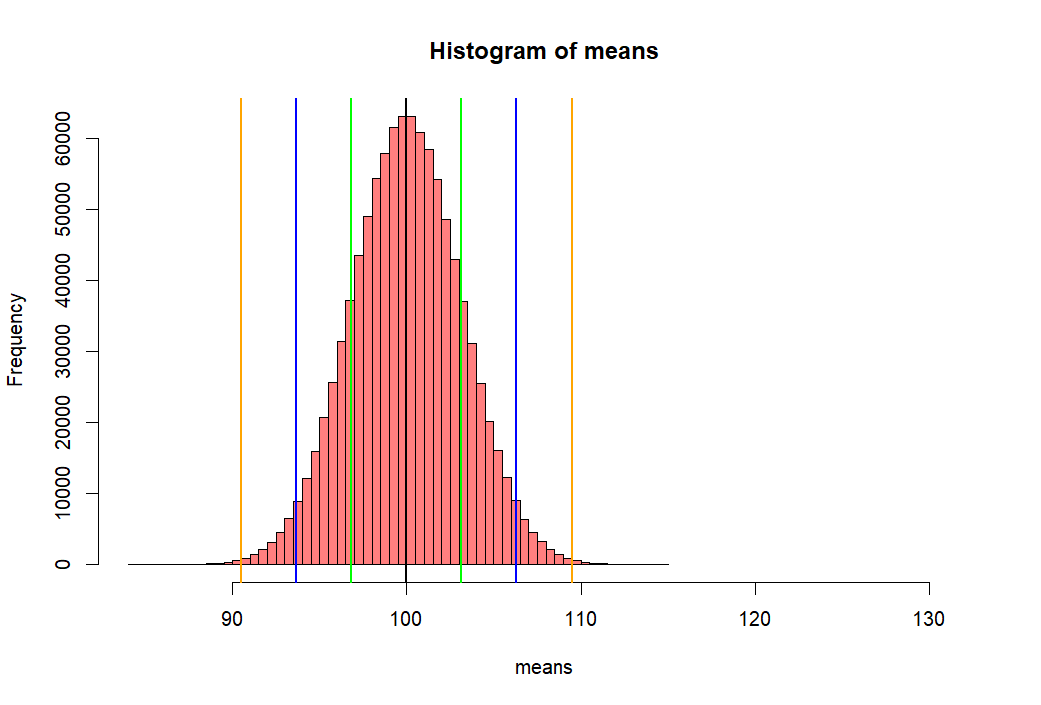
> lo1 <- mean(means)-se.s
> hi1 <- mean(means)+se.s
> lo2 <- mean(means)-2*se.s
> hi2 <- mean(means)+2*se.s
> lo3 <- mean(means)-3*se.s
> hi3 <- mean(means)+3*se.s

> hist(means, 
+      xlim = c(mean(means)-5*sd(means), mean(means)+10*sd(means)), 
+      col = rgb(1, 0, 0, .5))
> abline(v=mean(means), col="black", lwd=2)
> # abline(v=mean(p2), colo='darkgreen', lwd=3)
> abline(v=c(lo1, hi1, lo2, hi2, lo3, hi3), 
+        col=c("green","green", "blue", "blue", "orange", "orange"), 
+        lwd=2)
> 
> round(c(lo1, hi1))
[1]  97 103
> round(c(lo2, hi2))
[1]  94 106
> round(c(lo3, hi3))
[1]  91 109
> 
> round(c(loz1, hiz1))
[1]  97 103
> round(c(loz2, hiz2))
[1]  94 106
> round(c(loz3, hiz3))
[1]  91 109
> 

….

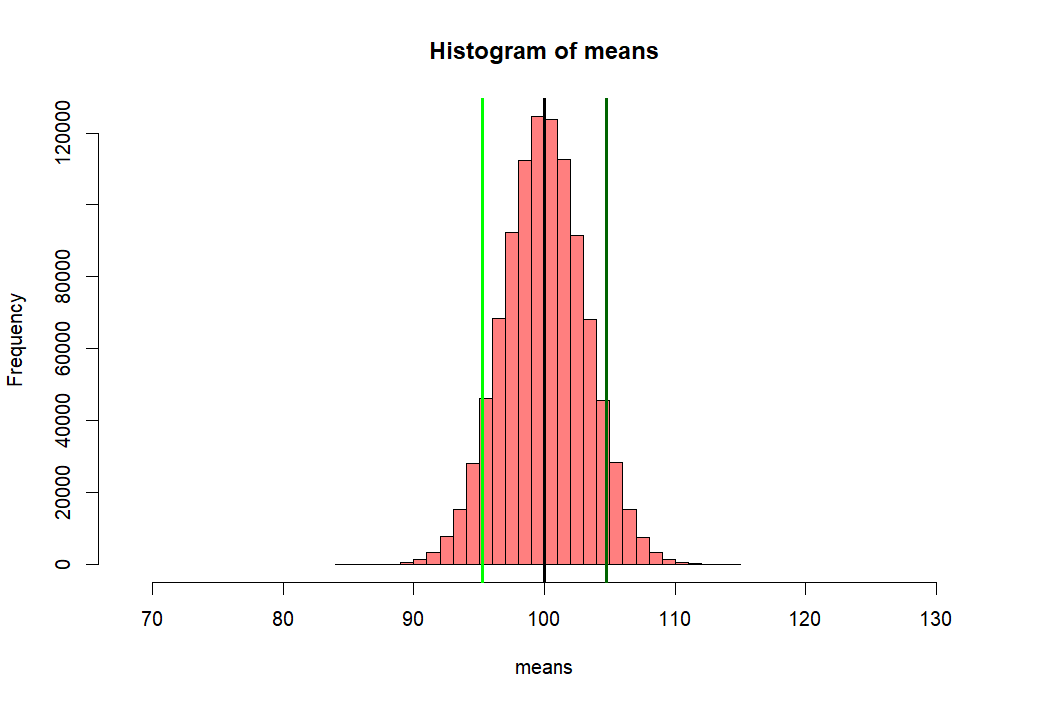
> m.sample.i.got <- mean(means)+ 1.5*sd(means)
> m.sample.i.got
[1] 104.7383
> 
> hist(means, 
+      xlim = c(mean(means)-10*sd(means), mean(means)+10*sd(means)), 
+      col = rgb(1, 0, 0, .5))
> abline(v=mean(means), col="black", lwd=3)
> abline(v=m.sample.i.got, col='darkgreen', lwd=3)
> 
> # what is the probablity of getting
> # greater than 
> # m.sample.i.got?
> m.sample.i.got
[1] 104.7383
> pnorm(m.sample.i.got, mean(means), sd(means), lower.tail = F)
[1] 0.0668072
> pnorm(m.sample.i.got, mean(p1), se.z, lower.tail = F)
[1] 0.06701819
> 
> # then, what is the probabilty of getting 
> # greater than m.sample.i.got and
> # less than corresponding value, which is
> # mean(means) - m.sample.i.got - mean(means)
> # (green line)
> tmp <- mean(means) - (m.sample.i.got - mean(means))
> tmp
[1] 95.26505
> abline(v=tmp, col='green', lwd=3)
> 2 * pnorm(m.sample.i.got, mean(p1), sd(means), lower.tail = F)
[1] 0.1339882
> m.sample.i.got
[1] 104.7383
> 

….

• 만약에 내가 한 샘플을 취해서 평균값을 살펴보니
• m.sample.i.got 값이었다고 하자 (104.7383).
• 이 값보다 큰 값이거나 아니면
• 이 값에 해당하는 평균 반대편 값보다 작은 값이 값이
• 나올 확률은 무엇인가?
• 즉, 녹색선과 연두색 선 바깥 쪽 부분의 probability 값은?
• 아래처럼 구해서 13.4% 정도가 된다
• 즉, 모집단 p1에서
• 무작위로 샘플링을 하여 (see sampling and probability sampling)
• s.size의 (10) 샘플을 취했는데 그 샘플의 평균이
• 104.7383 점보다 크거나 혹은
• 95.26505 점보다 작을 확률은 13.4% 이다.

> 2 * pnorm(m.sample.i.got, mean(p1), sd(means), lower.tail = F)
[1] 0.1339882

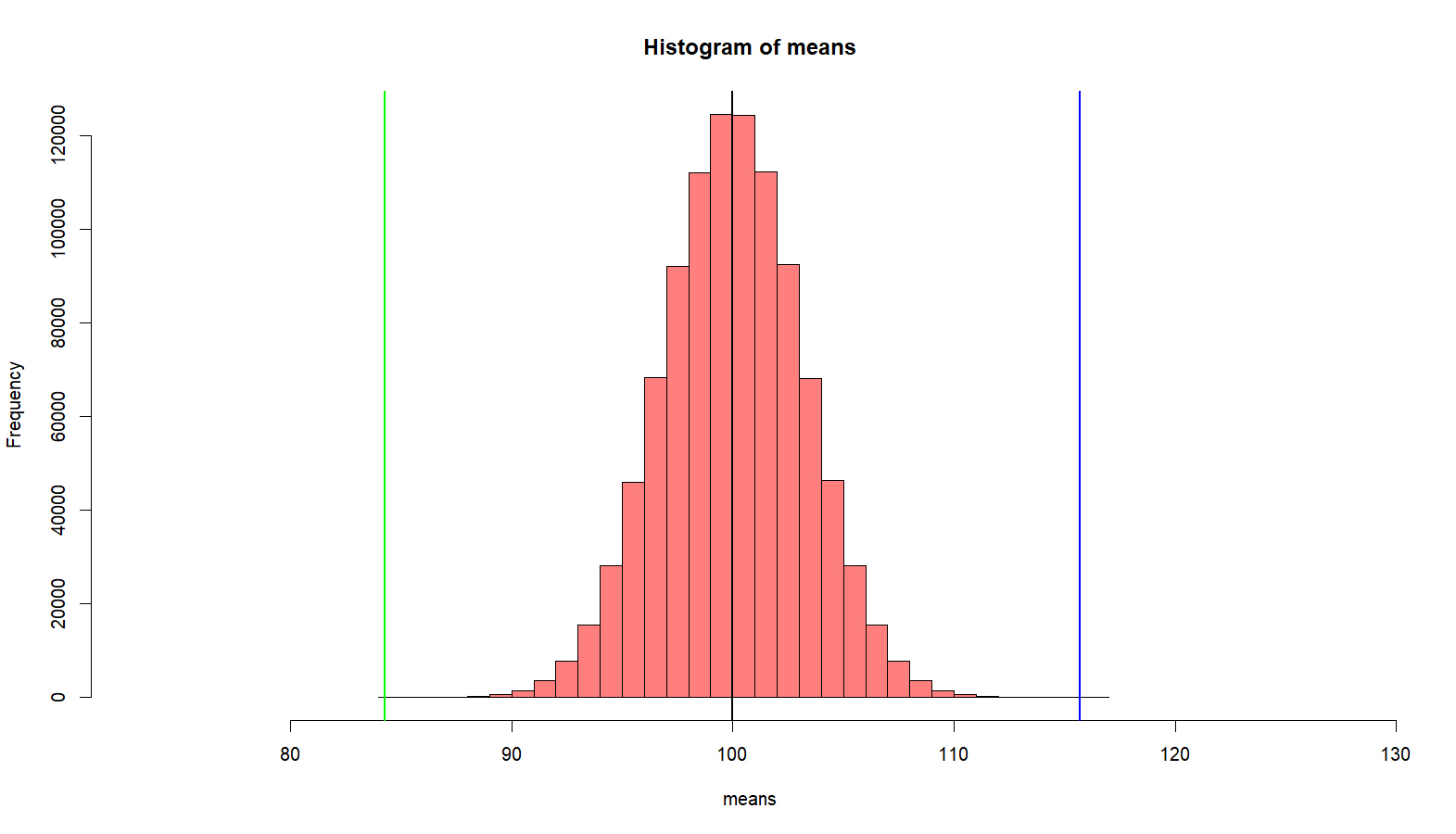
> ### one more time 
> mean(p2)
[1] 120
> sd(p2)
[1] 10
> sample(p2, s.size)
 [1] 105.57868  94.91021 117.73624 118.05456 118.65741 126.66806 136.65185 117.02986
 [9] 116.41683 105.91887
> m.sample.i.got <- mean(sample(p2, s.size))
> m.sample.i.got
[1] 114.155
> temp <- mean(means) - (m.sample.i.got-mean(means))
> temp 
[1] 85.84835
> hist(means, breaks=30, 
+      xlim = c(temp-4*sd(means), m.sample.i.got+4*sd(means)), 
+      col = rgb(1, 0, 0, .5))
> abline(v=mean(means), col="black", lwd=2)
> abline(v=m.sample.i.got, col='green', lwd=2)
> abline(v=temp, col='blue', lwd=2)
> # what is the probablity of getting
> # greater than 
> # m.sample.i.got?
> m.sample.i.got
[1] 114.155
> pnorm(m.sample.i.got, mean(p1), sd(means), lower.tail = F)
[1] 3.820806e-06
> # then, what is the probabilty of getting 
> # greater than m.sample.i.got and
> # less than corresponding value, which is
> # mean(means) - m.sample.i.got - mean(means)
> # (green line)
> tmp <- mean(means) - (m.sample.i.got - mean(means))
> abline(v=tmp, col='green', lwd=2)
> 2 * pnorm(m.sample.i.got, mean(p1), sd(means), lower.tail = F)
[1] 7.641611e-06
> 

….
다른 모집단에서 온 샘플 (sample from other population, p2)
이전 처럼 10명을 샘플로 뽑는데, p2에서 뽑는다. 따라서 이 샘플의 평균은 114.155 이다. 그런데 연구자는 이 샘플이 나온 모집단은 전혀 모르는 상태이다. 모집단의 평균도 모르고 분산값도 모른다. 그냥 10명을 샘플로 뽑았고, 이들이 p1에서 나왔을 확률을 알아보려고 한다. 이를 알아보기 위해서 스크립트를 돌려 보니, blue와 green라인 밖의 범위가 나올 확률은 7.641611e-06로 0에 가깝다. 따라서, 이 샘플은 10명은 p1에 속한 원소가 아닌 다른 성격을 가진 원소이다.

위에서 p2의 parameter에 대해서 잘 모른다는 점에 주목하라. 그리고 아래 시나리오를 상상하라.
어느 한 모집단의 IQ 평균이 100 이고 표준편차가 10 임을 알고 있다. 확률과통계 교수는 머리가 좋아지는 약을 개발하여 이를 팔아보려고 하고 있다. 이를 위해서 확통교수는 10을 뽑아서 머리가 좋아지는 약을 복용하도록 한 후에 IQ를 측정하였다. 그런데, 그 IQ 평균이 114.155 이다. 이 점수를 가지고 약의 효과가 있는지 검증을 해보력고 한다.