Table of Contents
Two-way ANOVA
Factorial ANOVA
rm(list=ls(all=TRUE))
#################################################
# two-way anova
# subject = factor(paste('sub', 1:30, sep=''))
#################################################
n.a.group <- 3 # a treatment 숫자 e.g: drug a1, a2, a3
n.b.group <- 2 # b 그룹 숫자 e.g.: exercise no(b1), yes(b2)
n.sub <- 30 # 총 샘플 숫자
n.sub/n.a.group
# 데이터 생성
set.seed(9)
a <- gl(n.a.group,
n.sub/n.a.group,
n.sub,
labels=c('drg1', 'drg2', 'drg3'))
b <- gl(n.b.group,
(n.sub/n.a.group)/2,
n.sub,
labels=c('noex', 'exerc'))
a
b
y <- rnorm(30, mean=10) +
3.14 * (a=='drg1' & b=='exerc') +
1.43 * (a=='drg3' & b=='exerc')
y
dat <- data.frame(a, b, y)
dat
# aov.dat <- aov(y~a*b) # anova test
# summary(aov.dat) # summary of the test output
# hand calculation
table(a,b)
tapply(y, list(a,b), mean) # 각 셀에서의 평균
tapply(y, a, mean)
tapply(y, b, mean)
n.within.each <- tapply(y, list(a,b), length) # the same as table(a, b)
n.within.each
df.within.each <- n.within.each - 1 # 각 셀에서의 샘플숫자
df.within.each
df.within <- sum(df.within.each) # df within
df.within
var.within <- tapply(y, list(a,b), var) # var.within
var.within
ss.within.each <- tapply(y, list(a,b), var) * df.within.each
ss.within.each
ss.within <- sum(ss.within.each) # ss.within
ss.within
ms.within <- ss.within / df.within
ms.within
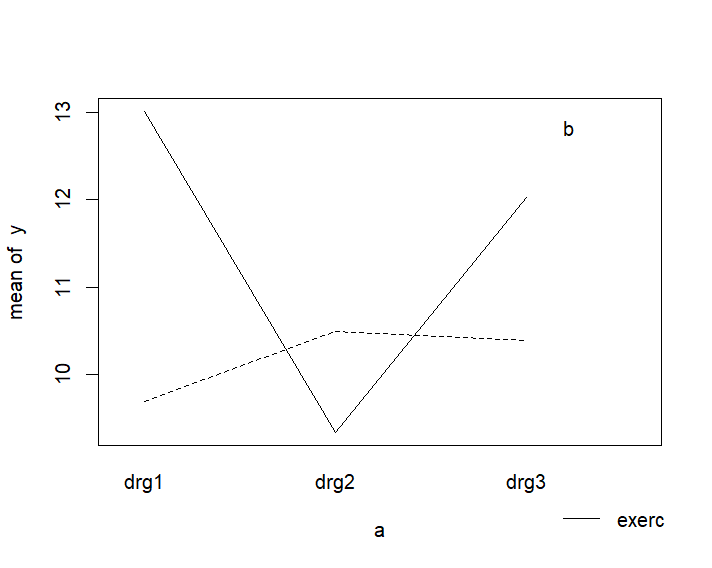
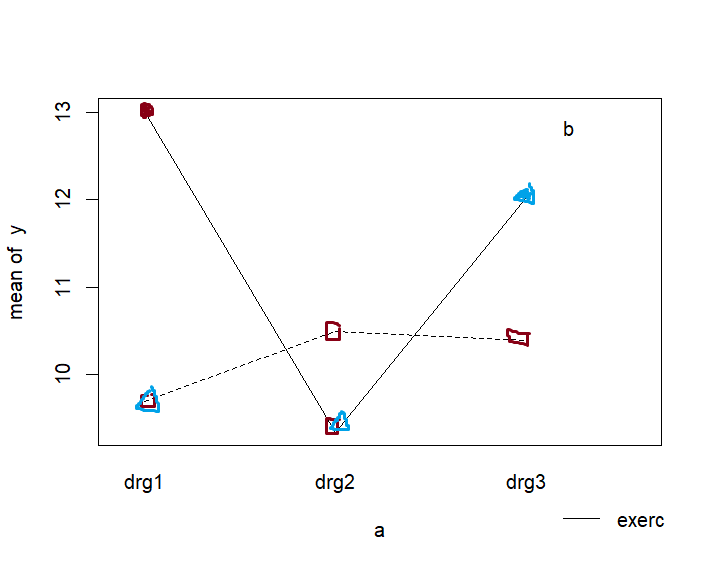
# interaction.plot(a,b,y)
mean.a <- tapply(y, list(a), mean)
mean.b <- tapply(y, list(b), mean)
mean.a
mean.b
var.a <- tapply(y, list(a), var)
var.b <- tapply(y, list(b), var)
var.a
var.b
mean.tot <- mean(dat$y)
var.tot <- var(dat$y)
df.tot <- n.sub - 1
ss.tot <- var.tot * df.tot
ms.tot <- ss.tot/df.tot
mean.tot
var.tot
df.tot
ss.tot
ms.tot
ss.tot/df.tot
## between
mean.each <- tapply(y, list(a,b), mean)
mean.each
mean.tot <- mean(y)
mean.tot
n.each <- tapply(y, list(a,b), length)
n.a.each <- tapply(y, list(a), length)
n.b.each <- tapply(y, list(b), length)
n.each
n.a.each
n.b.each
ss.bet <- sum(n.each*(mean.each-mean.tot)^2)
ss.bet
ss.tot
ss.within
ss.bet
ss.bet + ss.within
ss.a <- sum(n.a.each * ((mean.tot - mean.a)^2))
ss.b <- sum(n.b.each * ((mean.tot - mean.b)^2))
ss.a
ss.b
ss.ab <- ss.bet - (ss.a + ss.b) # ss.ab = ss.interaction
ss.ab
ss.tot
ss.bet
ss.within
ss.a
ss.b
ss.ab
df.tot <- n.sub - 1
df.bet <- (n.a.group * n.b.group) - 1
df.a <- n.a.group - 1
df.b <- n.b.group - 1
df.ab <- df.bet - (df.a + df.b)
df.within <- sum(df.within.each)
df.tot
df.bet
df.a
df.b
df.ab
df.within
ms.tot <- ss.tot / df.tot # we did it above
ms.bet <- ss.bet / df.bet
ms.a <- ss.a / df.a
ms.b <- ss.b / df.b
ms.ab <- ss.ab / df.ab
ms.within <- ss.within / df.within
ms.tot
ms.bet
ms.within
ms.a
ms.b
ms.ab
f.a <- ms.a / ms.within
f.b <- ms.b / ms.within
f.ab <- ms.ab / ms.within
alpha <- .05
# confidence interval
ci <- 1 - alpha
f.a
# 봐야할 F분포표에서의 F-value
# qt 처럼 qf 사용
# qf(alpha, df.between, df.within, lower.tail=F) 처럼 사용
qf(ci, df.a, df.within) # or
qf(alpha, df.a, df.within, lower.tail = F)
# 혹은
# qf(alpha, df.a, df.within, lower.tail = F)
# 도 마찬가지
f.a.crit <- qf(ci, df.a, df.within)
f.a > f.a.crit # 만약 f.a가 크다면
# 혹은 f.a 값에 해당하는 percentage를 구하면
pf(f.a, df.a, df.within, lower.tail = F)
f.b
qf(ci, df.b, df.within)
f.b > qf(ci, df.b, df.within)
pf(f.b, df.b, df.within, lower.tail = F)
f.ab
qf(ci, df.ab, df.within)
f.ab > qf(ci, df.ab, df.within)
pf(f.ab, df.ab, df.within, lower.tail = F)
# aov result
aov.dat.all <- aov(y ~ a * b, data = dat) # anova test
summary(aov.dat.all) # summary of the test output
aov.dat.noint <- aov(y ~ a + b, data = dat)
# interaction이 갖는 SS와 df를 residuals이 갖음을 주목
summary(aov.dat.noint)
aov.dat.all2 <- aov(y ~ a + b + a:b, data = dat)
summary(aov.dat.all2)
aov.dat.all # what is standard error of residuals
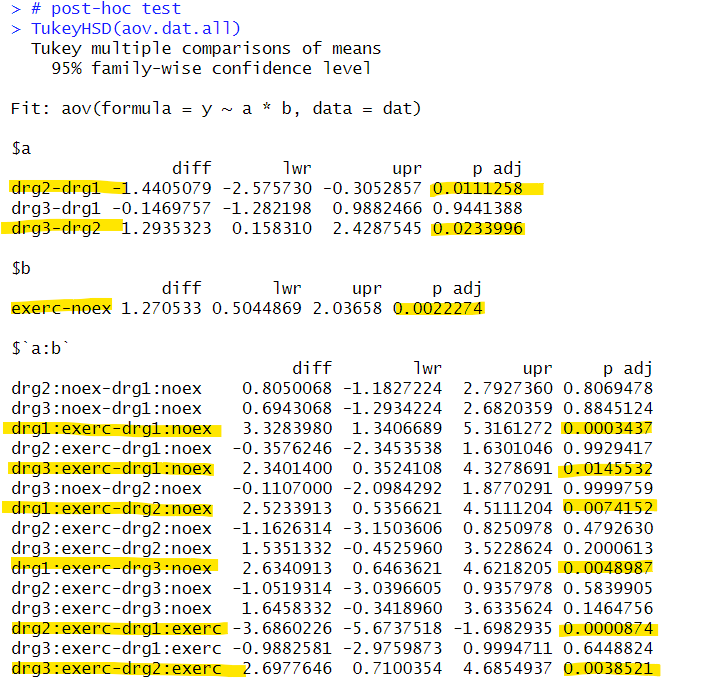
# post-hoc test
TukeyHSD(aov.dat.all)
TukeyHSD(aov.dat.all, which = "a")
TukeyHSD(aov.dat.all, which = "b")
TukeyHSD(aov.dat.all, which = "a:b")
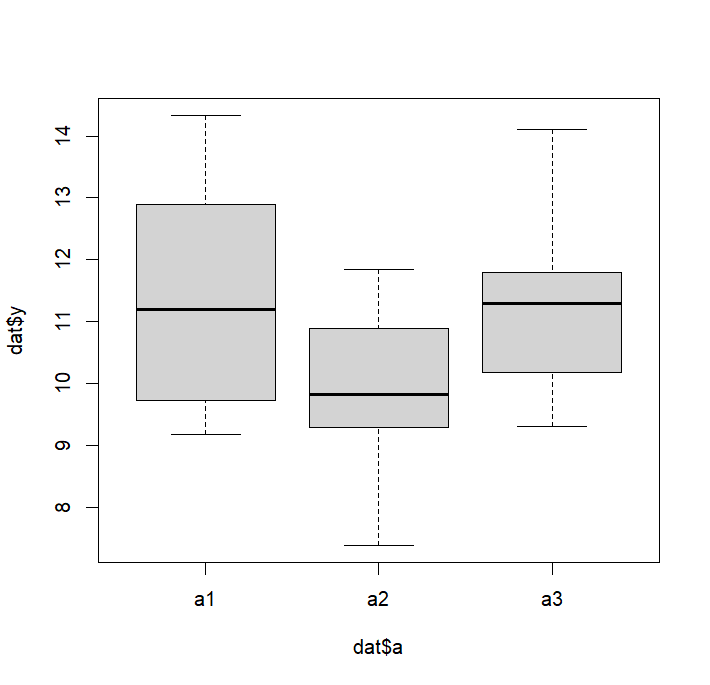
boxplot(dat$y~dat$a)
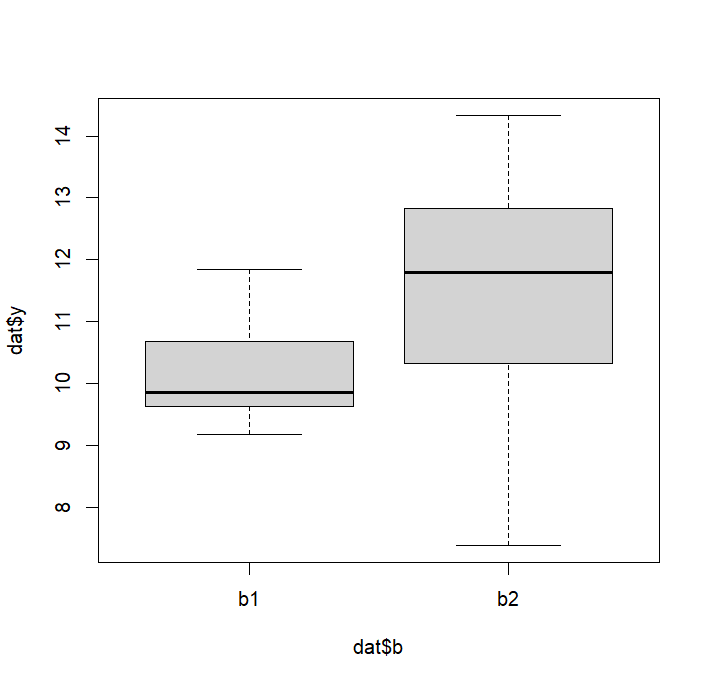
boxplot(dat$y~dat$b)
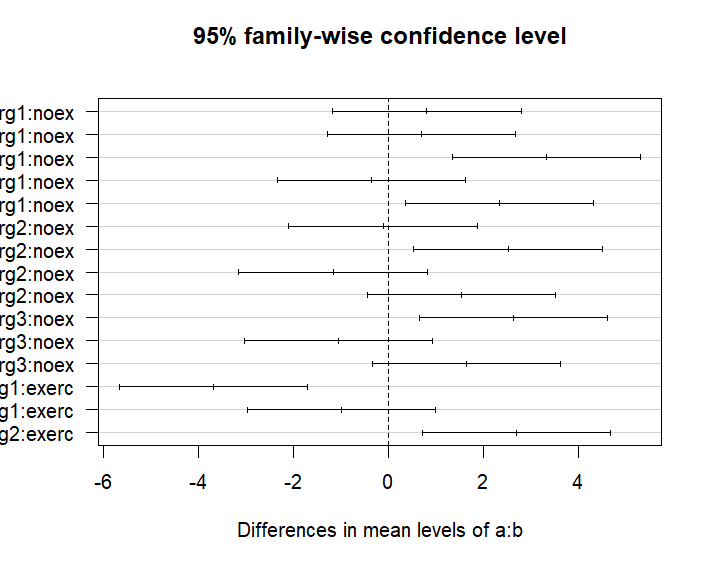
plot(TukeyHSD(aov.dat.all, which = "a:b"),
las = 2 # rotate x-axis ticks
)
#
#
# see another e.g. at
# https://statsandr.com/blog/two-way-anova-in-r/
#
#
Output, two-way ANOVA
> rm(list=ls(all=TRUE))
>
> #################################################
> # two-way anova
> # subject = factor(paste('sub', 1:30, sep=''))
> #################################################
>
> n.a.group <- 3 # a treatment 숫자 e.g: drug a1, a2, a3
> n.b.group <- 2 # b 그룹 숫자 e.g.: exercise no(b1), yes(b2)
> n.sub <- 30 # 총 샘플 숫자
> n.sub/n.a.group
[1] 10
>
> # 데이터 생성
> set.seed(9)
> a <- gl(n.a.group,
+ n.sub/n.a.group,
+ n.sub,
+ labels=c('drg1', 'drg2', 'drg3'))
> b <- gl(n.b.group,
+ (n.sub/n.a.group)/2,
+ n.sub,
+ labels=c('noex', 'exerc'))
> a
[1] drg1 drg1 drg1 drg1 drg1 drg1 drg1 drg1 drg1 drg1 drg2 drg2 drg2 drg2 drg2 drg2 drg2 drg2 drg2 drg2 drg3
[22] drg3 drg3 drg3 drg3 drg3 drg3 drg3 drg3 drg3
Levels: drg1 drg2 drg3
> b
[1] noex noex noex noex noex exerc exerc exerc exerc exerc noex noex noex noex noex exerc exerc exerc
[19] exerc exerc noex noex noex noex noex exerc exerc exerc exerc exerc
Levels: noex exerc
> y <- rnorm(30, mean=10) +
+ 3.14 * (a=='drg1' & b=='exerc') +
+ 1.43 * (a=='drg3' & b=='exerc')
> y
[1] 9.233204 9.183542 9.858465 9.722395 10.436307 11.953127 14.331987 13.121810 12.891915 12.777063
[11] 11.277571 9.531103 10.071054 9.733962 11.845257 9.160550 9.922552 7.382294 10.887884 9.292509
[21] 11.756993 10.182252 9.733111 10.926422 9.306668 14.111990 11.652524 10.723328 11.847213 11.799557
>
> dat <- data.frame(a, b, y)
> dat
a b y
1 drg1 noex 9.233204
2 drg1 noex 9.183542
3 drg1 noex 9.858465
4 drg1 noex 9.722395
5 drg1 noex 10.436307
6 drg1 exerc 11.953127
7 drg1 exerc 14.331987
8 drg1 exerc 13.121810
9 drg1 exerc 12.891915
10 drg1 exerc 12.777063
11 drg2 noex 11.277571
12 drg2 noex 9.531103
13 drg2 noex 10.071054
14 drg2 noex 9.733962
15 drg2 noex 11.845257
16 drg2 exerc 9.160550
17 drg2 exerc 9.922552
18 drg2 exerc 7.382294
19 drg2 exerc 10.887884
20 drg2 exerc 9.292509
21 drg3 noex 11.756993
22 drg3 noex 10.182252
23 drg3 noex 9.733111
24 drg3 noex 10.926422
25 drg3 noex 9.306668
26 drg3 exerc 14.111990
27 drg3 exerc 11.652524
28 drg3 exerc 10.723328
29 drg3 exerc 11.847213
30 drg3 exerc 11.799557
> # aov.dat <- aov(y~a*b) # anova test
> # summary(aov.dat) # summary of the test output
>
> # hand calculation
> table(a,b)
b
a noex exerc
drg1 5 5
drg2 5 5
drg3 5 5
> tapply(y, list(a,b), mean) # 각 셀에서의 평균
noex exerc
drg1 9.686782 13.015181
drg2 10.491789 9.329158
drg3 10.381089 12.026922
> tapply(y, a, mean)
drg1 drg2 drg3
11.350981 9.910474 11.204006
> tapply(y, b, mean)
noex exerc
10.18655 11.45709
> n.within.each <- tapply(y, list(a,b), length) # the same as table(a, b)
> n.within.each
noex exerc
drg1 5 5
drg2 5 5
drg3 5 5
> df.within.each <- n.within.each - 1 # 각 셀에서의 샘플숫자
> df.within.each
noex exerc
drg1 4 4
drg2 4 4
drg3 4 4
> df.within <- sum(df.within.each) # df within
> df.within
[1] 24
>
> var.within <- tapply(y, list(a,b), var) # var.within
> var.within
noex exerc
drg1 0.2628787 0.7362999
drg2 1.0308917 1.6504481
drg3 0.9510727 1.5677577
> ss.within.each <- tapply(y, list(a,b), var) * df.within.each
> ss.within.each
noex exerc
drg1 1.051515 2.945200
drg2 4.123567 6.601793
drg3 3.804291 6.271031
> ss.within <- sum(ss.within.each) # ss.within
> ss.within
[1] 24.7974
>
> ms.within <- ss.within / df.within
> ms.within
[1] 1.033225
>
> # interaction.plot(a,b,y)
>
> mean.a <- tapply(y, list(a), mean)
> mean.b <- tapply(y, list(b), mean)
> mean.a
drg1 drg2 drg3
11.350981 9.910474 11.204006
> mean.b
noex exerc
10.18655 11.45709
>
> var.a <- tapply(y, list(a), var)
> var.b <- tapply(y, list(b), var)
> var.a
drg1 drg2 drg3
3.521366 1.567182 1.871915
> var.b
noex exerc
0.7773781 3.7300196
>
> mean.tot <- mean(dat$y)
> var.tot <- var(dat$y)
> df.tot <- n.sub - 1
> ss.tot <- var.tot * df.tot
> ms.tot <- ss.tot/df.tot
>
> mean.tot
[1] 10.82182
> var.tot
[1] 2.593465
> df.tot
[1] 29
> ss.tot
[1] 75.21048
> ms.tot
[1] 2.593465
> ss.tot/df.tot
[1] 2.593465
>
>
> ## between
> mean.each <- tapply(y, list(a,b), mean)
> mean.each
noex exerc
drg1 9.686782 13.015181
drg2 10.491789 9.329158
drg3 10.381089 12.026922
> mean.tot <- mean(y)
> mean.tot
[1] 10.82182
> n.each <- tapply(y, list(a,b), length)
> n.a.each <- tapply(y, list(a), length)
> n.b.each <- tapply(y, list(b), length)
> n.each
noex exerc
drg1 5 5
drg2 5 5
drg3 5 5
> n.a.each
drg1 drg2 drg3
10 10 10
> n.b.each
noex exerc
15 15
>
>
>
> ss.bet <- sum(n.each*(mean.each-mean.tot)^2)
> ss.bet
[1] 50.41308
>
> ss.tot
[1] 75.21048
> ss.within
[1] 24.7974
> ss.bet
[1] 50.41308
> ss.bet + ss.within
[1] 75.21048
>
> ss.a <- sum(n.a.each * ((mean.tot - mean.a)^2))
> ss.b <- sum(n.b.each * ((mean.tot - mean.b)^2))
> ss.a
[1] 12.5663
> ss.b
[1] 12.10691
> ss.ab <- ss.bet - (ss.a + ss.b) # ss.ab = ss.interaction
> ss.ab
[1] 25.73987
>
> ss.tot
[1] 75.21048
> ss.bet
[1] 50.41308
> ss.within
[1] 24.7974
> ss.a
[1] 12.5663
> ss.b
[1] 12.10691
> ss.ab
[1] 25.73987
>
> df.tot <- n.sub - 1
> df.bet <- (n.a.group * n.b.group) - 1
> df.a <- n.a.group - 1
> df.b <- n.b.group - 1
> df.ab <- df.bet - (df.a + df.b)
> df.within <- sum(df.within.each)
>
> df.tot
[1] 29
> df.bet
[1] 5
> df.a
[1] 2
> df.b
[1] 1
> df.ab
[1] 2
> df.within
[1] 24
>
> ms.tot <- ss.tot / df.tot # we did it above
> ms.bet <- ss.bet / df.bet
> ms.a <- ss.a / df.a
> ms.b <- ss.b / df.b
> ms.ab <- ss.ab / df.ab
> ms.within <- ss.within / df.within
>
> ms.tot
[1] 2.593465
> ms.bet
[1] 10.08262
> ms.within
[1] 1.033225
> ms.a
[1] 6.283151
> ms.b
[1] 12.10691
> ms.ab
[1] 12.86993
>
>
> f.a <- ms.a / ms.within
> f.b <- ms.b / ms.within
> f.ab <- ms.ab / ms.within
>
> alpha <- .05
> # confidence interval
> ci <- 1 - alpha
>
> f.a
[1] 6.081107
> # 봐야할 F분포표에서의 F-value
> # qt 처럼 qf 사용
> # qf(alpha, df.between, df.within, lower.tail=F) 처럼 사용
> qf(ci, df.a, df.within) # or
[1] 3.402826
> qf(alpha, df.a, df.within, lower.tail = F)
[1] 3.402826
> # 혹은
> # qf(alpha, df.a, df.within, lower.tail = F)
> # 도 마찬가지
> f.a.crit <- qf(ci, df.a, df.within)
> f.a > f.a.crit # 만약 f.a가 크다면
[1] TRUE
> # 혹은 f.a 값에 해당하는 percentage를 구하면
> pf(f.a, df.a, df.within, lower.tail = F)
[1] 0.007302552
>
> f.b
[1] 11.7176
> qf(ci, df.b, df.within)
[1] 4.259677
> f.b > qf(ci, df.b, df.within)
[1] TRUE
> pf(f.b, df.b, df.within, lower.tail = F)
[1] 0.00222738
>
> f.ab
[1] 12.45608
> qf(ci, df.ab, df.within)
[1] 3.402826
> f.ab > qf(ci, df.ab, df.within)
[1] TRUE
> pf(f.ab, df.ab, df.within, lower.tail = F)
[1] 0.0001947745
>
> # aov result
> aov.dat.all <- aov(y ~ a * b, data = dat) # anova test
> summary(aov.dat.all) # summary of the test output
Df Sum Sq Mean Sq F value Pr(>F)
a 2 12.57 6.283 6.081 0.007303 **
b 1 12.11 12.107 11.718 0.002227 **
a:b 2 25.74 12.870 12.456 0.000195 ***
Residuals 24 24.80 1.033
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
> aov.dat.noint <- aov(y ~ a + b, data = dat)
> # interaction이 갖는 SS와 df를 residuals이 갖음을 주목
> summary(aov.dat.noint)
Df Sum Sq Mean Sq F value Pr(>F)
a 2 12.57 6.283 3.233 0.0558 .
b 1 12.11 12.107 6.229 0.0192 *
Residuals 26 50.54 1.944
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
> aov.dat.all2 <- aov(y ~ a + b + a:b, data = dat)
> summary(aov.dat.all2)
Df Sum Sq Mean Sq F value Pr(>F)
a 2 12.57 6.283 6.081 0.007303 **
b 1 12.11 12.107 11.718 0.002227 **
a:b 2 25.74 12.870 12.456 0.000195 ***
Residuals 24 24.80 1.033
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
> aov.dat.all # what is standard error of residuals
Call:
aov(formula = y ~ a * b, data = dat)
Terms:
a b a:b Residuals
Sum of Squares 12.56630 12.10691 25.73987 24.79740
Deg. of Freedom 2 1 2 24
Residual standard error: 1.016477
Estimated effects may be unbalanced
>
> # post-hoc test
> TukeyHSD(aov.dat.all)
Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = y ~ a * b, data = dat)
$a
diff lwr upr p adj
drg2-drg1 -1.4405079 -2.575730 -0.3052857 0.0111258
drg3-drg1 -0.1469757 -1.282198 0.9882466 0.9441388
drg3-drg2 1.2935323 0.158310 2.4287545 0.0233996
$b
diff lwr upr p adj
exerc-noex 1.270533 0.5044869 2.03658 0.0022274
$`a:b`
diff lwr upr p adj
drg2:noex-drg1:noex 0.8050068 -1.1827224 2.7927360 0.8069478
drg3:noex-drg1:noex 0.6943068 -1.2934224 2.6820359 0.8845124
drg1:exerc-drg1:noex 3.3283980 1.3406689 5.3161272 0.0003437
drg2:exerc-drg1:noex -0.3576246 -2.3453538 1.6301046 0.9929417
drg3:exerc-drg1:noex 2.3401400 0.3524108 4.3278691 0.0145532
drg3:noex-drg2:noex -0.1107000 -2.0984292 1.8770291 0.9999759
drg1:exerc-drg2:noex 2.5233913 0.5356621 4.5111204 0.0074152
drg2:exerc-drg2:noex -1.1626314 -3.1503606 0.8250978 0.4792630
drg3:exerc-drg2:noex 1.5351332 -0.4525960 3.5228624 0.2000613
drg1:exerc-drg3:noex 2.6340913 0.6463621 4.6218205 0.0048987
drg2:exerc-drg3:noex -1.0519314 -3.0396605 0.9357978 0.5839905
drg3:exerc-drg3:noex 1.6458332 -0.3418960 3.6335624 0.1464756
drg2:exerc-drg1:exerc -3.6860226 -5.6737518 -1.6982935 0.0000874
drg3:exerc-drg1:exerc -0.9882581 -2.9759873 0.9994711 0.6448824
drg3:exerc-drg2:exerc 2.6977646 0.7100354 4.6854937 0.0038521
> TukeyHSD(aov.dat.all, which = "a")
Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = y ~ a * b, data = dat)
$a
diff lwr upr p adj
drg2-drg1 -1.4405079 -2.575730 -0.3052857 0.0111258
drg3-drg1 -0.1469757 -1.282198 0.9882466 0.9441388
drg3-drg2 1.2935323 0.158310 2.4287545 0.0233996
> TukeyHSD(aov.dat.all, which = "b")
Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = y ~ a * b, data = dat)
$b
diff lwr upr p adj
exerc-noex 1.270533 0.5044869 2.03658 0.0022274
> TukeyHSD(aov.dat.all, which = "a:b")
Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = y ~ a * b, data = dat)
$`a:b`
diff lwr upr p adj
drg2:noex-drg1:noex 0.8050068 -1.1827224 2.7927360 0.8069478
drg3:noex-drg1:noex 0.6943068 -1.2934224 2.6820359 0.8845124
drg1:exerc-drg1:noex 3.3283980 1.3406689 5.3161272 0.0003437
drg2:exerc-drg1:noex -0.3576246 -2.3453538 1.6301046 0.9929417
drg3:exerc-drg1:noex 2.3401400 0.3524108 4.3278691 0.0145532
drg3:noex-drg2:noex -0.1107000 -2.0984292 1.8770291 0.9999759
drg1:exerc-drg2:noex 2.5233913 0.5356621 4.5111204 0.0074152
drg2:exerc-drg2:noex -1.1626314 -3.1503606 0.8250978 0.4792630
drg3:exerc-drg2:noex 1.5351332 -0.4525960 3.5228624 0.2000613
drg1:exerc-drg3:noex 2.6340913 0.6463621 4.6218205 0.0048987
drg2:exerc-drg3:noex -1.0519314 -3.0396605 0.9357978 0.5839905
drg3:exerc-drg3:noex 1.6458332 -0.3418960 3.6335624 0.1464756
drg2:exerc-drg1:exerc -3.6860226 -5.6737518 -1.6982935 0.0000874
drg3:exerc-drg1:exerc -0.9882581 -2.9759873 0.9994711 0.6448824
drg3:exerc-drg2:exerc 2.6977646 0.7100354 4.6854937 0.0038521
> boxplot(dat$y~dat$a)
> boxplot(dat$y~dat$b)
> plot(TukeyHSD(aov.dat.all, which = "a:b"),
+ las = 2 # rotate x-axis ticks
+ )
>
>
> #
> #
> # see another e.g. at
> # https://statsandr.com/blog/two-way-anova-in-r/
> #
> #
>
>
output interpretation
상호작용효과 포함 해석
- drug1의 효과에 운동의 역할은 아주 중요한 것으로 밝혀졌다.
- 반면에 drug2, 3에 한해서는 운동의 역할은 제한적이었다.
- 특히 drg3의 경우 운동이 효과를 증대시키기는 하였지만 그것이 통계학적으로 의미있는 것은 아니었다.
- 또한 drg2의 경우 운동이 오히려 효과를 감소하는 것으로 나타났다. 그렇지만 이 또한 통계학적으로 의미가 있는 것은 아니었다.
- 이를 통해서 drg1을 처치받는 환자의 경우에는 운동을 꼭 하도록 하여야 함을 알 수 있고
- drg2의 경우에는 그 효과가 미미하므로 권장을 하는 정도가 필요함을 알 수 있었다.
혹은
- drg1과 운동이 병행 된 경우에는 대부분의 다른 처방보다 월등한 효과가 있는 것으로 밝혀졌다.
- 운동이 병행된 drg1과 drg3의 효과에는 차이가 없었다.
- drg2의 운동유무, 그리고 drg3의 운동을 하지않음과 통계학적으로 유의미한 차이가 있었다.