rnorm2 <- function(n,mean,sd) { mean+sd*scale(rnorm(n)) }
set.seed(1001)
df <- rnorm2(600000, 100, 10)
head(df)

n <- 1600
iter <- 10000
means <- rep (NA, iter)
for(i in 1:iter){
  means[i] = mean(sample(df, n))
}
# means
hist(means)
mean(means)
sd(means)

m.the <- 100
se.the <- 10/sqrt(n)
m.the
se.the

s.s <-107.5
p.val <- (m.the-s.s)/se.the
p.val <- pnorm(p.val)
p.val

# proportions
#
p <- 0.55 # 민경욱 지지율 가정정
q <- 1-p

set.seed(101)
el <- sample.int(2, 400000, replace=TRUE, prob=c(p, q))
table(el)
prop.table(table(el))

n <- 16000
iter <- 10000
els <- rep (NA, iter)
prop <- rep (NA, iter)
for(i in 1:iter){
  els <- sample(el, n, replace=FALSE)
  prop[i] <- table(els)[1]/(table(els)[1]+table(els)[2])
}
# els
head(prop)
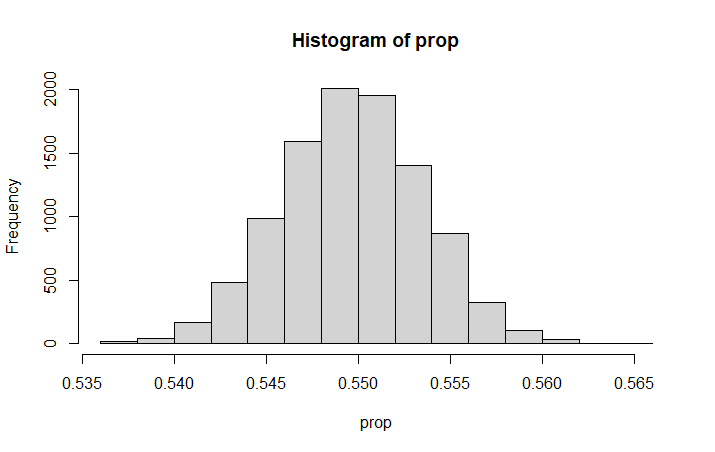
hist(prop)


pre.vote <- 0.430
m.emp <- mean(prop)
m.theo <- p
m.emp 
m.theo

se.emp <- sd(prop)
se.theo <- sqrt((p*q)/n)
se.emp
se.theo


m.theo
pre.vote
m.theo-pre.vote
se.theo
# install.packages("Rmpfr")

library(Rmpfr)
.N <- function(.) mpfr(., precBits = 100)

zval <- (m.theo-pre.vote)/se.theo
zval
p.val <- pnorm(zval, lower.tail = F)
p.val # limit in 1e-217 

p.lot <- 1/1000000 # lotto를 맞을 확률을 100만분의 1이라고 하면
p.lot^21*7 # lotto를 연거퍼서 21일동안 맞을 확률의 일곱배배; not 지구나이 . . . . 

> # proportions
> #
> p <- 0.55 # 민경욱 지지율 가정정
> q <- 1-p
> set.seed(101)
> el <- sample.int(2, 400000, replace=TRUE, prob=c(p, q))
> table(el)
el
     1      2 
219878 180122 
> prop.table(table(el))
el
       1        2 
0.549695 0.450305 
> n <- 16000
> iter <- 10000
> els <- rep (NA, iter)
> prop <- rep (NA, iter)
> for(i in 1:iter){
+   els <- sample(el, n, replace=FALSE)
+   prop[i] <- table(els)[1]/(table(els)[1]+table(els)[2])
+ }
> # els
> head(prop)
[1] 0.5461250 0.5512500 0.5465000 0.5473125 0.5539375 0.5563125
> hist(prop)
> pre.vote <- 0.430
> m.emp <- mean(prop)
> m.theo <- p
> m.emp 
[1] 0.5497185
> m.theo
[1] 0.55
> se.emp <- sd(prop)
> se.theo <- sqrt((p*q)/n)
> se.emp
[1] 0.003837126
> se.theo
[1] 0.003933033
> m.theo
[1] 0.55
> pre.vote
[1] 0.43
> m.theo-pre.vote
[1] 0.12
> se.theo
[1] 0.003933033
> library(Rmpfr)
> .N <- function(.) mpfr(., precBits = 100)
> zval <- (m.theo-pre.vote)/se.theo
> zval
[1] 30.5108
> p.val <- pnorm(zval, lower.tail = F)
> p.val # limit in 1e-217 
[1] 9.368078e-205
> p.lot <- 1/1000000 # lotto를 맞을 확률을 100만분의 1이라고 하면
> p.lot^21*7 # lotto를 연거퍼서 21일동안 맞을 확률의 일곱배배; not 지구나이 . . . . 
[1] 7e-126
>