1.
cardat <- data.frame(mtcars$mpg, mtcars$am)
names(cardat) <- c("mpg", "am")
OR.
cardat=subset(mtcars,select=c(mpg,am))
2.
cardat$am <- as.factor(cardat$am)
3.
levels(cardat$am) <- c("auto", "man")
Or
2. 3,4.
cardat$am <- factor(cardat$am, labels=c("auto", "man"))
5,6.
> var.test(cardat$mpg~cardat$am)
F test to compare two variances
data: cardat$mpg by cardat$am
F = 0.38656, num df = 18, denom df = 12, p-value = 0.06691
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
0.1243721 1.0703429
sample estimates:
ratio of variances
0.3865615
p value가 0.05보다 크므로 두 집단 간에 분산에 차이가
없을 것이라는 영가설을 부정하지 못한다. 즉 두 집단 간
분산에는 차이가 없다라고 할 수 있다.
7,8.
위에서 밝힌 것처럼 집단 간 분산에 차이가 없으로므,
var.equal=T 를 사용하여 t-test를 수행한다.
> t.test(cardat$mpg ~ cardat$am ,var.equal = T)
Two Sample t-test
data: cardat$mpg by cardat$am
t = -4.1061, df = 30, p-value = 0.000285
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-10.84837 -3.64151
sample estimates:
mean in group auto mean in group man
17.14737 24.39231
t-test결과 p 값이 0.001 보다 작으므로 두 집단 간에 차이가 있다라고
판단할 수 있다. 즉, automatric과 manual 간에 mileage(mpg)에는
통계학적인 차이가 있다 (t(30) = -4.106, p < .001).
9.
> donuts<-read.csv("http://commres.net/wiki/_media/r/donuts.txt",header = T,sep="\t")
> donuts
Fat1 Fat2 Fat3 Fat4
1 164 178 175 155
2 172 191 193 166
3 168 197 178 149
4 177 182 171 164
5 156 185 163 170
6 195 177 176 168
10.
> sdonuts<-stack(donuts)
> sdonuts
values ind
1 164 Fat1
2 172 Fat1
3 168 Fat1
4 177 Fat1
5 156 Fat1
6 195 Fat1
7 178 Fat2
8 191 Fat2
9 197 Fat2
10 182 Fat2
11 185 Fat2
12 177 Fat2
13 175 Fat3
14 193 Fat3
15 178 Fat3
16 171 Fat3
17 163 Fat3
18 176 Fat3
19 155 Fat4
20 166 Fat4
21 149 Fat4
22 164 Fat4
23 170 Fat4
24 168 Fat4
11.
level별 평균은 tapply펑션을 이용하여 한꺼번에
구한다.
> tapply(sdonuts$values,sdonuts$ind,mean)
Fat1 Fat2 Fat3 Fat4
172 185 176 162
12.
> s.mod<-aov(sdonuts$values~sdonuts$ind)
> summary(s.mod)
Df Sum Sq Mean Sq F value Pr(>F)
sdonuts$ind 3 1636 545.5 5.406 0.00688 **
Residuals 20 2018 100.9
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
->F test값이 5.406이고 P value가 0.001 보다 작으므로
도넛의 종류에 따라 기름의 함유량에는 차이가 있다라고
볼 수 있다 (F(3,20) = 5.406, p < 0.001).
구체적으로 어느 집단간의 차이가 나는지는
post hoc test가 필요하다.
13.
545.5
14.
100.9
15.
> baskball<-read.csv("http://commres.net/wiki/_media/r/baskball.csv")
> baskball
Time Shoes Made
1 Morning Others 28
2 Morning Others 30
3 Night Others 35
4 Night Others 34
5 Morning Favorite 32
6 Morning Favorite 34
7 Night Favorite 40
8 Night Favorite 38
9 Morning Others 32
10 Morning Others 30
11 Night Others 33
12 Night Others 35
13 Morning Favorite 35
14 Morning Favorite 32
15 Night Favorite 35
16 Night Favorite 34
17 Morning Favorite 32
18 Morning Favorite 33
19 Night Favorite 35
20 Night Favorite 38
21 Morning Others 33
22 Morning Others 30
23 Night Others 33
24 Night Others 30
25 Morning Favorite 30
26 Morning Favorite 25
27 Night Favorite 38
28 Night Favorite 41
29 Morning Others 32
30 Morning Others 33
31 Night Others 33
32 Night Others 30
>
16.
tapply(baskball$Made,baskball$Time,mean)
Morning Night
31.3125 35.1250
> tapply(baskball$Made,baskball$Shoes,mean)
Favorite Others
34.5000 31.9375
17.
> tapply(baskball$Made,baskball$Shoes,sd)
Favorite Others
4.016632 2.048373
> tapply(baskball$Made,baskball$Time,sd)
Morning Night
2.441823 3.180671
18.
총 3개의 가설을 검증할 수 있다 (두 개의 주효과와
하나의 상호작용효과).
주효과
H1:Shoes에 따라 Made에 차이가 있을 것이다.
H2:Time에 따라 Made에 차이가 있을 것이다.
상호작용효과
H3:Shoes와 Time 의 상호작용에 따라 Made에 차이가 있을 것이다.
19.
> b.mod<-aov(baskball$Made~baskball$Time*baskball$Shoes)
> summary(b.mod)
Df Sum Sq Mean Sq F value Pr(>F)
baskball$Time 1 116.28 116.28 20.526 1e-04 ***
baskball$Shoes 1 52.53 52.53 9.273 0.00502 **
baskball$Time:baskball$Shoes 1 30.03 30.03 5.301 0.02896 *
Residuals 28 158.62 5.67
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
>
>
->Time,Shoes,그리고 상호작용 F 값에 대응하는 p 값이 각각
0.001, 0.01, 0.05보다 작으므로 각 가설이 모두 검증된다.
1. Shoes에따라 자유투의 성공횟수에 차이가 있을 것이다 (F(1, 28) = 20.526, p < .001).
2. Time에 따라 자유투의 성공횟수에 차이가 있을 것이다 (F(1, 28) = 9.273, p < .01).
3. Shoes와 Time의 상호작용의 성공횟수에 영향을 미칠 것이다 (F(1, 28) = 5.301, p < .05).
20.
post hoc test를 할 필요가 없다.
각 독립변인의 level이 2가지이므로 각 lelvel의 차이는
평균을 살펴보는 것으로 충분하게 된다.
21,22
favorite shoes를 신은 경우와, others를 신은 경우에 자유투 성공
횟수의 차이가 Time(시간)에 따라서 각각 다르게 나타난다고 할 수
있다.
23.
> library(MASS)
> cats
Sex Bwt Hwt
1 F 2.0 7.0
2 F 2.0 7.4
3 F 2.0 9.5
4 F 2.1 7.2
5 F 2.1 7.3
6 F 2.1 7.6
7 F 2.1 8.1
8 F 2.1 8.2
9 F 2.1 8.3
10 F 2.1 8.5
11 F 2.1 8.7
12 F 2.1 9.8
13 F 2.2 7.1
14 F 2.2 8.7
15 F 2.2 9.1
16 F 2.2 9.7
17 F 2.2 10.9
18 F 2.2 11.0
19 F 2.3 7.3
20 F 2.3 7.9
21 F 2.3 8.4
22 F 2.3 9.0
23 F 2.3 9.0
24 F 2.3 9.5
25 F 2.3 9.6
26 F 2.3 9.7
27 F 2.3 10.1
28 F 2.3 10.1
29 F 2.3 10.6
30 F 2.3 11.2
31 F 2.4 6.3
32 F 2.4 8.7
33 F 2.4 8.8
34 F 2.4 10.2
35 F 2.5 9.0
36 F 2.5 10.9
37 F 2.6 8.7
38 F 2.6 10.1
39 F 2.6 10.1
40 F 2.7 8.5
41 F 2.7 10.2
42 F 2.7 10.8
43 F 2.9 9.9
44 F 2.9 10.1
45 F 2.9 10.1
46 F 3.0 10.6
47 F 3.0 13.0
48 M 2.0 6.5
49 M 2.0 6.5
50 M 2.1 10.1
51 M 2.2 7.2
52 M 2.2 7.6
53 M 2.2 7.9
54 M 2.2 8.5
55 M 2.2 9.1
56 M 2.2 9.6
57 M 2.2 9.6
58 M 2.2 10.7
59 M 2.3 9.6
60 M 2.4 7.3
61 M 2.4 7.9
62 M 2.4 7.9
63 M 2.4 9.1
64 M 2.4 9.3
65 M 2.5 7.9
66 M 2.5 8.6
67 M 2.5 8.8
68 M 2.5 8.8
69 M 2.5 9.3
70 M 2.5 11.0
71 M 2.5 12.7
72 M 2.5 12.7
73 M 2.6 7.7
74 M 2.6 8.3
75 M 2.6 9.4
76 M 2.6 9.4
77 M 2.6 10.5
78 M 2.6 11.5
79 M 2.7 8.0
80 M 2.7 9.0
81 M 2.7 9.6
82 M 2.7 9.6
83 M 2.7 9.8
84 M 2.7 10.4
85 M 2.7 11.1
86 M 2.7 12.0
87 M 2.7 12.5
88 M 2.8 9.1
89 M 2.8 10.0
90 M 2.8 10.2
91 M 2.8 11.4
92 M 2.8 12.0
93 M 2.8 13.3
94 M 2.8 13.5
95 M 2.9 9.4
96 M 2.9 10.1
97 M 2.9 10.6
98 M 2.9 11.3
99 M 2.9 11.8
100 M 3.0 10.0
101 M 3.0 10.4
102 M 3.0 10.6
103 M 3.0 11.6
104 M 3.0 12.2
105 M 3.0 12.4
106 M 3.0 12.7
107 M 3.0 13.3
108 M 3.0 13.8
109 M 3.1 9.9
110 M 3.1 11.5
111 M 3.1 12.1
112 M 3.1 12.5
113 M 3.1 13.0
114 M 3.1 14.3
115 M 3.2 11.6
116 M 3.2 11.9
117 M 3.2 12.3
118 M 3.2 13.0
119 M 3.2 13.5
120 M 3.2 13.6
121 M 3.3 11.5
122 M 3.3 12.0
123 M 3.3 14.1
124 M 3.3 14.9
125 M 3.3 15.4
126 M 3.4 11.2
127 M 3.4 12.2
128 M 3.4 12.4
129 M 3.4 12.8
130 M 3.4 14.4
131 M 3.5 11.7
132 M 3.5 12.9
133 M 3.5 15.6
134 M 3.5 15.7
135 M 3.5 17.2
136 M 3.6 11.8
137 M 3.6 13.3
138 M 3.6 14.8
139 M 3.6 15.0
140 M 3.7 11.0
141 M 3.8 14.8
142 M 3.8 16.8
143 M 3.9 14.4
144 M 3.9 20.5
> summary(cats)
Sex Bwt Hwt
F:47 Min. :2.000 Min. : 6.30
M:97 1st Qu.:2.300 1st Qu.: 8.95
Median :2.700 Median :10.10
Mean :2.724 Mean :10.63
3rd Qu.:3.025 3rd Qu.:12.12
Max. :3.900 Max. :20.50
> class(cats)
[1] "data.frame"
cats 데이터는 Sex라는 2가지 level(F,M)을 갖는 Factor와
Bwt와 Hwt라는 숫자로 이루어진 vector변수로 이루어져있는
dataframe 형식의 데이터이며, hwt와 bwt는 각각 heart
weight와 body weight를 의미하며, Sex의 F, M은 각각 female과
male을 의미한다.
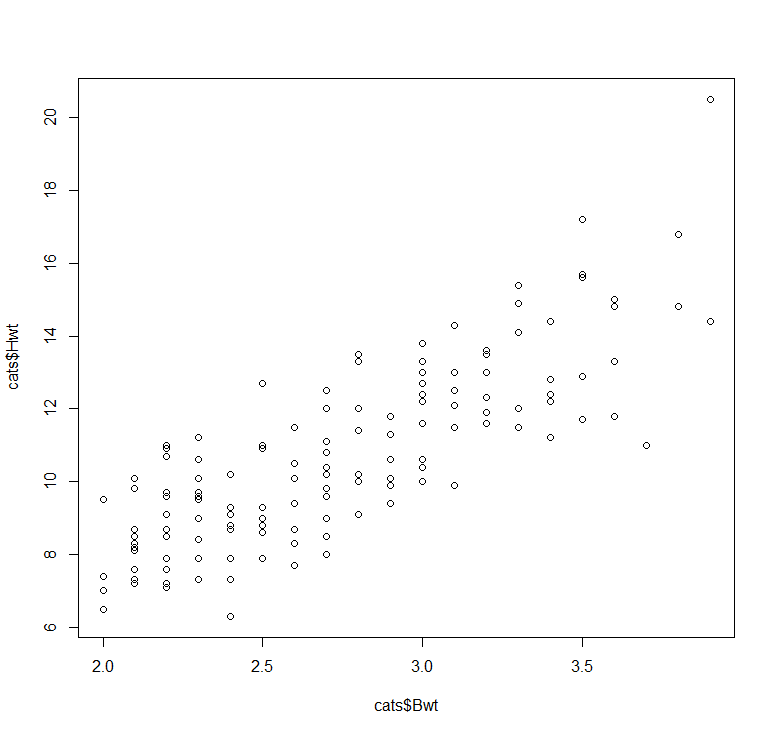
24.
plot(cats$Bwt,cats$Hwt)
아래 그림 참조
25, 26.
> c.lm<-lm(cats$Hwt~cats$Bwt)
> summary(c.lm)
Call:
lm(formula = cats$Hwt ~ cats$Bwt)
Residuals:
Min 1Q Median 3Q Max
-3.5694 -0.9634 -0.0921 1.0426 5.1238
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.3567 0.6923 -0.515 0.607
cats$Bwt 4.0341 0.2503 16.119 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.452 on 142 degrees of freedom
Multiple R-squared: 0.6466, Adjusted R-squared: 0.6441
F-statistic: 259.8 on 1 and 142 DF, p-value: < 2.2e-16
Bwt는 Hwt에 영향을 미친다고 할 수 있다 (F(1, 142) = 259.8,
p < 0.001). Bwt는 Hwt의 총 분산 중 약 65%를 (0.6466) 설명
한다.
27.
0.6466
28.
64.66%
29.
abline(c.lm,col="red")
아래 그림 참조
30, 31.
30,31.
> st.lm<-lm(st$Murder~st$Population+st$Income+st$Illiteracy)
> summary(st.lm)
Call:
lm(formula = st$Murder ~ st$Population + st$Income + st$Illiteracy)
Residuals:
Min 1Q Median 3Q Max
-4.7846 -1.6768 -0.0839 1.4783 7.6417
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.3402721 3.3694210 0.398 0.6926
st$Population 0.0002219 0.0000842 2.635 0.0114 *
st$Income 0.0000644 0.0006762 0.095 0.9245
st$Illiteracy 4.1109188 0.6706786 6.129 1.85e-07 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.507 on 46 degrees of freedom
Multiple R-squared: 0.5669, Adjusted R-squared: 0.5387
F-statistic: 20.07 on 3 and 46 DF, p-value: 1.84e-08
먼저 F값의 p-value를 통해 통계적으로 유의미한 모델임을 알 수 있다. 즉,
Population, Income, Illiteracy가 Murder에 영향을 주는 것으로 판단
할 수 있다 (F(3,46) = 20.07, p < .001). 또한 세개의 독립변수(예측변인)은
종속변인 Murder의 총 분산 중 약 57% (0.5669)를 설명하는데 기여한다.
각 변인의 기여도를 보면 Population과 Illiteracy의 t-value에 해당하느
p 값은 0.05보다 작으므로 유의미한 기여를 한다고 판달 할 수 있다. 그러나,
Income의 경우 p 값이 0.9245로 0.05보다 커서 유의미한 기여를 한다고 볼 수
없다.
32.
R square = 0.5669
종속변인인 Murder의 분산 중 독립변인인 세가지 변인(Population,
Income,Illiteracy)으로 인해 설명되는정도라고 볼 수 있다.
23.
29.


