Table of Contents
Measuring Central Tendency
mean
read mean document
\begin{equation*} \text{Sum of all elements} = X_1 + X_2 + X_3 + X_4 + X_5 + . . . + X_n \\ \end{equation*}
위의 sum of all elements는 아래와 같이 표현된 수 있다.
\begin{equation*} X_1 + X_2 + X_3 + X_4 + X_5 + . . . + X_n = \sum\limits_{i=1}^{n} X_i \end{equation*}
위의 sum of all elements를 n으로 나누는 것이 평균
\begin{equation*} \frac{\sum\limits_{i=1}^{n} X_i}{n} \end{equation*}
이것을 우리는 흔히 “무”라고 부른다.
\begin{equation*}
\mu = \frac{\sum\limits_{i=1}^{N} X_i}{N}
\end{equation*}
| age | 19 | 20 | 21 |
| freq | 1 | 3 | 1 |
위처럼 frequency로 정리된 표는 아래와 같이 계산할 수 있다.
\begin{equation*} \begin{split} \mu = \frac{\sum\limits_{}^{} \text{fx}}{\sum{\text{f.nothing}}} = \frac{1 \text{x} 19 + 3 \text{x} 20 + 1 \text{x} 21}{5} \end{split} \end{equation*}
outlier
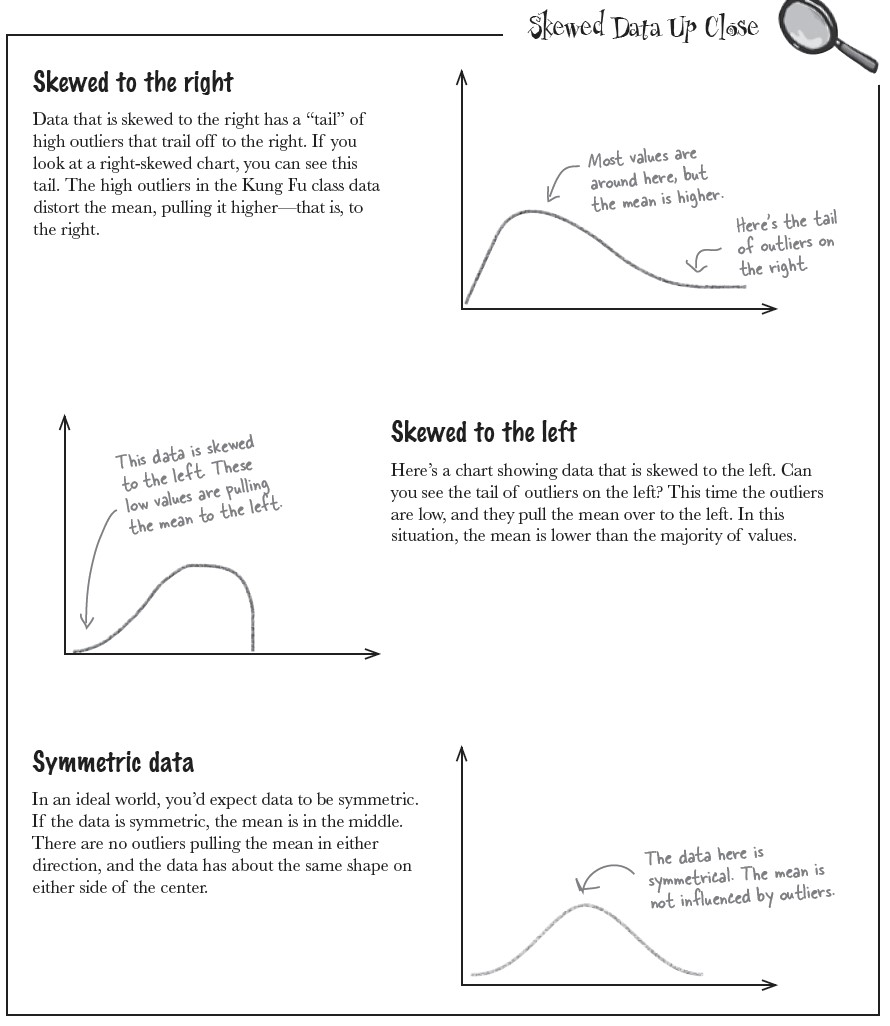
skewedness
median
see median document
{19, 19, 20, 20, 20, 21, 21, 100, 102}
{19, 20, 20, 20, 21, 21, 100, 102}
see also quartile document
e.g.
one <- c(1,1,1,1,2,2,2,2,2,2,3,3,3,3,4,4,4,4,5,5,5,6,6,7,8) two <- c(1,4,6,6,8,8,8,9,9,9,9,10,10,10,10,11,11,11,11,11,12,12,12,12,12)
> median(one) [1] 3 > mean(one) [1] 3.44 > median(two) [1] 10 > mean(two) [1] 9.28
> hist(one) > hist(two) > par(mfrow=c(1,2)) > hist(one) > hist(two)
par(mfrow=c(1,2))
hist(one)
abline(v=mean(one), col="blue", lty=1)
abline(v=median(one), col="red", lty=2)
legend(3.8,9.5, legend=c("mean", "median"), col=c("blue", "red"), lty=1:2, cex=.8)
hist(two)
abline(v=mean(two), col="blue", lty=1)
abline(v=median(two), col="red", lty=2)
legend(.5,9.5, legend=c("mean", "median"), col=c("blue", "red"), lty=1:2, cex=.8)
par(mfrow=c(1,1))
e.g. 1
quartile 명령어는 r에서는 없다. 대신 quantile을 사용한다. 둘은 비슷하나 quantile은 4분위 이상의 것을 한다.
교재에서 구하는 quartile방식은 알아두되, 실제에서는 R에서 quantile을 사용하여 quartile을 구하도록 한다. see quartile
R에서
temp <- c(19, 19, 20, 20, 20, 21, 21, 100, 102)
> quantile(temp) 0% 25% 50% 75% 100% 19 20 20 21 102 > quantile(temp, prob=1/4) 25% 20 > quantile(temp, prob=c(1/4,2/4)) 25% 50% 20 20 > quantile(temp, prob=seq(0,1,1/4)) 0% 25% 50% 75% 100% 19 20 20 21 102 > quantile(temp, prob=seq(0,1,1/2)) 0% 50% 100% 19 20 102 > median(temp) [1] 20 > > quantile(temp, prob=seq(0,1,1/8)) 0% 12.5% 25% 37.5% 50% 62.5% 75% 87.5% 100% 19 19 20 20 20 21 21 100 102
e.g. 2
- Get mean, median for each data set.
- State how each is skewed.
| value | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| freq | 4 | 6 | 4 | 4 | 3 | 2 | 1 | 1 |
| ser | value |
| 1 | 1 |
| 2 | 1 |
| 3 | 1 |
| 4 | 1 |
| 5 | 2 |
| 6 | 2 |
| 7 | 2 |
| 8 | 2 |
| 9 | 2 |
| 10 | 2 |
| 11 | 3 |
| 12 | 3 |
| 13 | 3 |
| 14 | 3 |
| 15 | 4 |
| 16 | 4 |
| 17 | 4 |
| 18 | 4 |
| 19 | 5 |
| 20 | 5 |
| 21 | 5 |
| 22 | 6 |
| 23 | 6 |
| 24 | 7 |
| 25 | 8 |
| median | |
| mode | |
| mean | |
| min | |
| 1st q | |
| 3rd q | |
| max |
> x <- c(1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 6, 6, 7, 8) > x [1] 1 1 1 1 2 2 2 2 2 2 3 3 3 3 4 4 4 4 5 5 5 6 6 7 8 >
> median(x) [1] 3 > mean(x) [1] 3.44 > min(x) [1] 1 > max(x) [1] 8 > quantile(x) 0% 25% 50% 75% 100% 1 2 3 5 8 >
{1, 1, 1, 2, 2, 2, 2, 3, 3, 31, 31, 32, 32, 32, 32, 33, 33, 33}
{1, 1, 1, 2, 2, 2, 2, 2, 3, 3, 31, 31, 32, 32, 32, 32, 33, 33, 33}
{1, 1, 1, 2, 2, 2, 2, 2, 3, 31, 31, 31, 32, 32, 32, 32, 33, 33, 33}
a <- c(1, 1, 1, 2, 2, 2, 2, 3, 3, 31, 31, 32, 32, 32, 32, 33, 33, 33) b <- c(1, 1, 1, 2, 2, 2, 2, 2, 3, 3, 31, 31, 32, 32, 32, 32, 33, 33, 33) c <- c(1, 1, 1, 2, 2, 2, 2, 2, 3, 31, 31, 31, 32, 32, 32, 32, 33, 33, 33) a b c length(a) length(b) length(c) mean(a) mean(b) mean(c) median(a) median(b) median(c)
# output > a <- c(1, 1, 1, 2, 2, 2, 2, 3, 3, 31, 31, 32, 32, 32, 32, 33, 33, 33) > b <- c(1, 1, 1, 2, 2, 2, 2, 2, 3, 3, 31, 31, 32, 32, 32, 32, 33, 33, 33) > c <- c(1, 1, 1, 2, 2, 2, 2, 2, 3, 31, 31, 31, 32, 32, 32, 32, 33, 33, 33) > a [1] 1 1 1 2 2 2 2 3 3 31 31 32 32 32 32 33 33 33 > b [1] 1 1 1 2 2 2 2 2 3 3 31 31 32 32 32 32 33 33 33 > c [1] 1 1 1 2 2 2 2 2 3 31 31 31 32 32 32 32 33 33 33 > length(a) [1] 18 > length(b) [1] 19 > length(c) [1] 19 > mean(a) [1] 17 > mean(b) [1] 16.21053 > mean(c) [1] 17.68421 > median(a) [1] 17 > median(b) [1] 3 > median(c) [1] 31 >
Ugliness of mean and median
## answer n <- 3+2+2 +3+4+4 n mean.duckc <- 17 median.duckc <- 17 tot <- mean.duckc * n # 2 :: 4 인것은 이미 알고 있음 known.sum <- (1*3)+(2*4)+(3*2)+(31*2) tot - known.sum # 227 = (32*4) + (33*3) 이므로 duckc <- c(1,1,1,2,2,2,2,3,3,31,31,32,32,32,32,33,33,33) mean(duckc) median(duckc)
## how do they change with 2 added and 31 added duckc.2.added <- c(1,1,1,2,2,2,2,2,3,3,31,31,32,32,32,32,33,33,33) mean(duckc.2.added) median(duckc.2.added) duckc.31.added <- c(1,1,1,2,2,2,2,3,3,31,31,31,32,32,32,32,33,33,33) mean(duckc.31.added) median(duckc.31.added)
mode
see mode document
modality
bimodal
trimodal
multimodal
unimodal
It works for both number measured and category measured data.
Measuring central tendency
커피전문점의 관대한 CEO는 직원의 연봉을 인상하기로 하였습니다. 그런데 연봉을 2000불씩 올려야 할지 혹은 10%씩 올려야 할 지 알 수가 없습니다. 직원들의 연봉 평균값은 50,000불이고, 중앙값은 20,000불입니다. 또한 최빈값은 10,000불입니다.
- 커피전문점 직원들의 연봉이 모두 2000불씩 오르면 평균값, 중앙값, 최빈값은 어떻게 변할까요?
- 커피전문점 직원들의 연봉이 모두 10%씩 오르면 평균, 중앙, 최빈값은 어떻게 변할까요?
- 평균값과 일치하는 급여를 받는 사람은 어느 쪽 인상을 선호할까요?
- 최빈값과 동일한 급여를 받고 있다면 어느쪽 인상을 선호할까요?
Mean
\begin{eqnarray*}
\mu & = & \frac {\Sigma {X_{i}}} {N} \\
& = & 50000 \\
\end{eqnarray*}
\begin{eqnarray*}
\text {2000 raised to the mean} & = & \frac {\sum{(X_{i} + 2000)}} {N} \\
& = & \frac {\sum{(X_{i})} + \sum{(2000)}} {N} \\
& = & \frac {\sum{(X_{i})}} {N} + \frac {N * (2000)} {N} \\
& = & 50000 + 2000 \\
& = & 52000
\end{eqnarray*}
Median
모든 연봉에 2000불을 더하는 것이므로 median 값의 위치는 변하지 않는다. 따라서
\begin{eqnarray*}
\text{Original Median} (20000) + 2000 & = & 22000
\end{eqnarray*}
Mode
모든 연봉에 2000불을 더하는 것이므로 mode 값은 원래 모드값인 10000 불에 2000불을 더한 값이다. 따라서
\begin{eqnarray*}
\text{Original Mode} (10000) + 2000 & = & 12000
\end{eqnarray*}
Mean
\begin{eqnarray*}
\text {10% raised to the mean} & = & \frac {\sum{(1.1 * X_{i})}} {N} \\
& = & \frac {1.1 * \sum{(X_{i})}} {N} \\
& = & 1.1 * \frac {\sum{(X_{i})}} {N} \\
& = & 1.1 * 50000 \\
& = & 55000
\end{eqnarray*}
Median
모든 연봉에 10%를 더하는 것이므로 median 값의 위치는 변하지 않는다. 따라서
\begin{eqnarray*}
\text{Original Median} (20000) * 1.1 & = & 22000
\end{eqnarray*}
Mode
모든 연봉에 10%를 더하는 것이므로 mode 값은 원래 모드값인 10000 불에 1.1을 곱한 값이다. 따라서
\begin{eqnarray*}
\text{Original Mode} (10000) * 1.1 & = & 11000
\end{eqnarray*}